• 정렬 (sorting): 어떤 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 것
• 정렬은 프로그램 작성시 빈번하게 필요로 함
• 다양한 알고리즘이 고안되었으며, 알고리즘 학습의 필수

버블 정렬

두 인접한 데이터를 비교해서, 앞에 있는 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘

(출처: 위키피디아)

def bubblesort(data):
    for index in range(len(data) - 1):
        swap = False
        for index2 in range(len(data) - index - 1):
            if data[index2] > data[index2 + 1]:
                data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
                swap = True
        
        if swap == False:
            break
    return data

삽입 정렬

key 값으로 앞에 정렬된 값들과 하나씩 비교해 순서에 맞는 곳에 삽입하는 정렬 알고리즘

def insertion_sort(data):
    for index in range(len(data) - 1):
        for index2 in range(index + 1, 0, -1):
            if data[index2] < data[index2 - 1]:
                data[index2], data[index2 - 1] = data[index2 - 1], data[index2]
            else:
                break
    return data

선택 정렬

stand 인덱스에 들어갈 값의 인덱스를 temp에 임시 저장하여 최종 선택된 temp인덱스에 있는 값을 현재 stand인덱스의 값과 바꾸며 정렬하는 알고리즘

def selection_sort(data):
    for stand in range(len(data) - 1):
        temp = stand
        for index in range(stand + 1, len(data)):
            if data[temp] > data[index]:
                temp = index
        data[temp], data[stand] = data[stand], data[temp]
    return data

병합 정렬

기본 케이스로 분할한 뒤 각각의 케이스를 정렬하여 병합해 전체를 정렬하는 알고리즘
(분할 정복 알고리즘과 재귀적인 방법을 이용한 정렬 알고리즘)

def merge(left, right):
    merged = list()
    left_point, right_point = 0, 0
    
    # case1 - left/right 둘다 있을때
    while len(left) > left_point and len(right) > right_point:
        if left[left_point] > right[right_point]:
            merged.append(right[right_point])
            right_point += 1
        else:
            merged.append(left[left_point])
            left_point += 1

    # case2 - left 데이터가 없을 때
    while len(left) > left_point:
        merged.append(left[left_point])
        left_point += 1
        
    # case3 - right 데이터가 없을 때
    while len(right) > right_point:
        merged.append(right[right_point])
        right_point += 1
    
    return merged


def mergesplit(data):
    if len(data) <= 1:
        return data
    medium = int(len(data) / 2)
    left = mergesplit(data[:medium])
    right = mergesplit(data[medium:])
    return merge(left, right)

힙 정렬

퀵 정렬

기준점(pivot)을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right) 으로 모으는 함수를 재귀적으로 사용하여 정렬하는 알고리즘

def qsort(data):
    if len(data) <= 1:
        return data
    
    pivot = data[0]

    left = [ item for item in data[1:] if pivot > item ]
    right = [ item for item in data[1:] if pivot <= item ]
    
    return qsort(left) + [pivot] + qsort(right)

알고리즘 별 시간 복잡도 분석

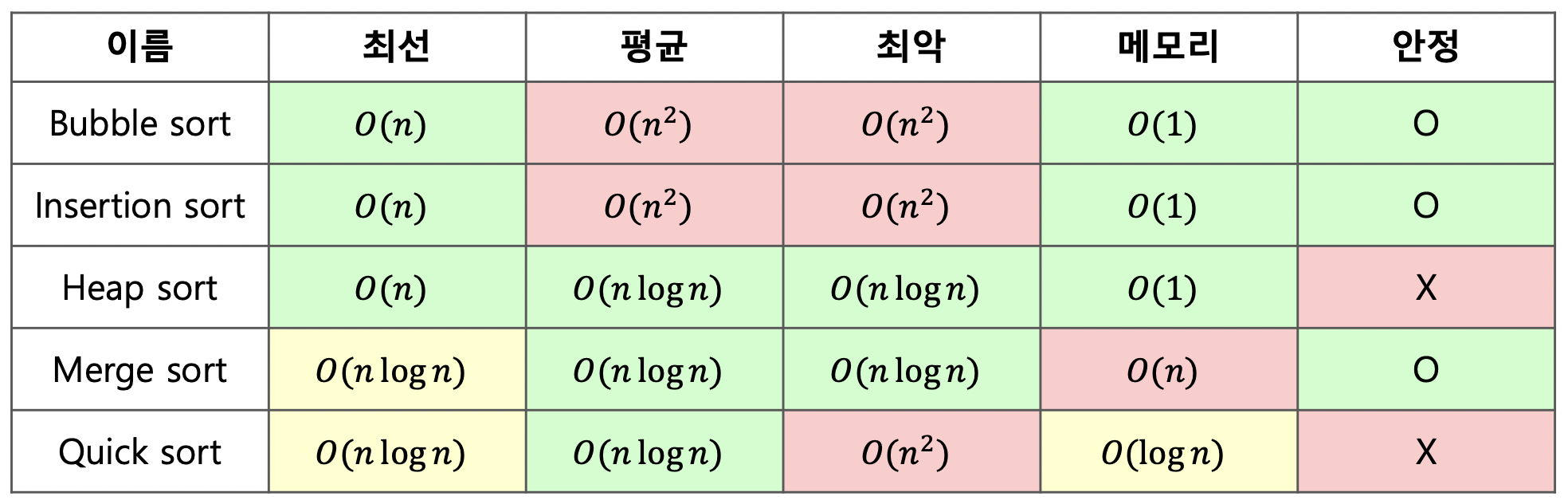
(출처: naver.d2)

정렬 알고리즘 관련한 좋은 포스팅

naver.d2-tim_sort