[Data_structure] 그래프

March 27, 2021

1. 그래프의 기초

1-1 그래프의 정의

데이터 간에 연결 관계가 있는 자료 구조 (ex. 위치 관계, 사회 관계)
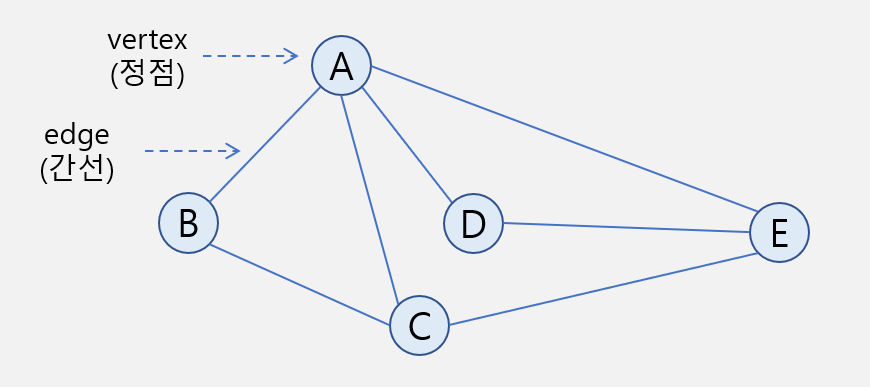
하나의 객체를 나타내는 vertex와 객체 간의 연결 관계를 나타내는 edge로 이루어져 있다.

1-2 그래프 특성

인접 : 두 노드(vertex)가 한 개의 엣지(edge)로 연결되어 있다. (B는 A, C와 인접해 있다)
연결 : 두 노드가 한 개 이상의 엣지로 연결되어 있다. (B는 A, C, D, E와 연결되어 있다)
차수 : 노드가 가지고 있는 엣지의 수 (B의 차수는 2이다)

1-3 그래프의 종류

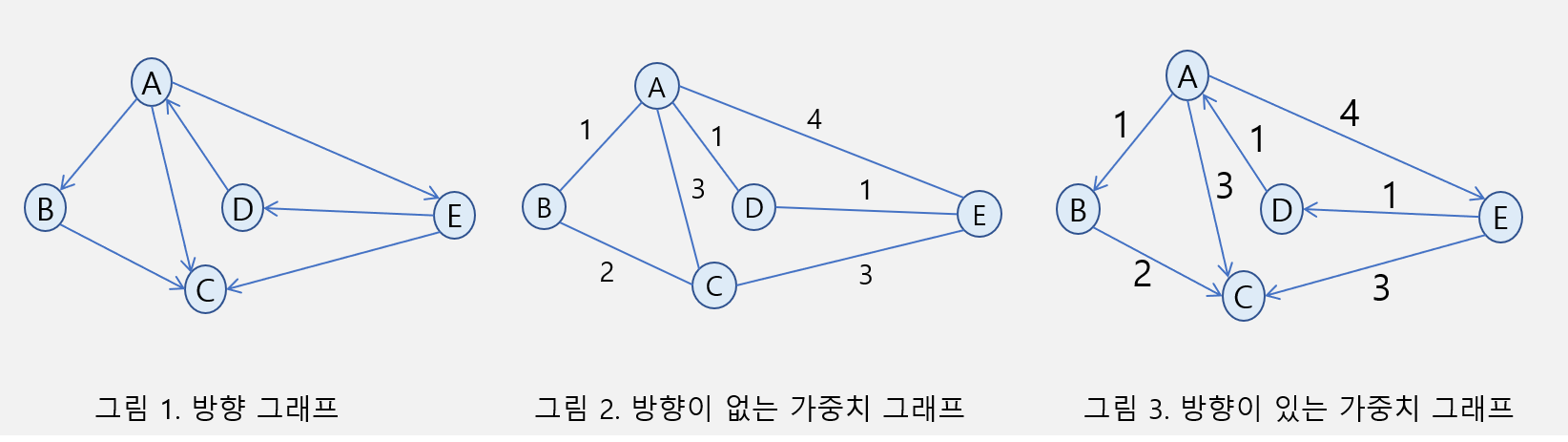
무방향 그래프 : 엣지에 방향성이 없다. (A,B) = (B,A)
방향 그래프 : 엣지에 방향성이 있다. (A,B) != (B,A)
가중치 그래프 : 엣지에 가중치가 있다.

1-4 그래프 구현

노드 표현하기

"""노드 클래스 생성"""
class GraphNode:
  def __init__(self, name):
    self.name = name
  
"""노드 객체 생성"""
node1 = GraphNode("A")
node2 = GraphNode("B")
node3 = GraphNode("C")

"""그래프에 노드 입력"""
graph = [node1, node2, node3]

엣지 표현하기
그래프에 넣은 노드들의 관계를 나타내는 엣지를 구현하는 방법에는 두 가지가 있다.

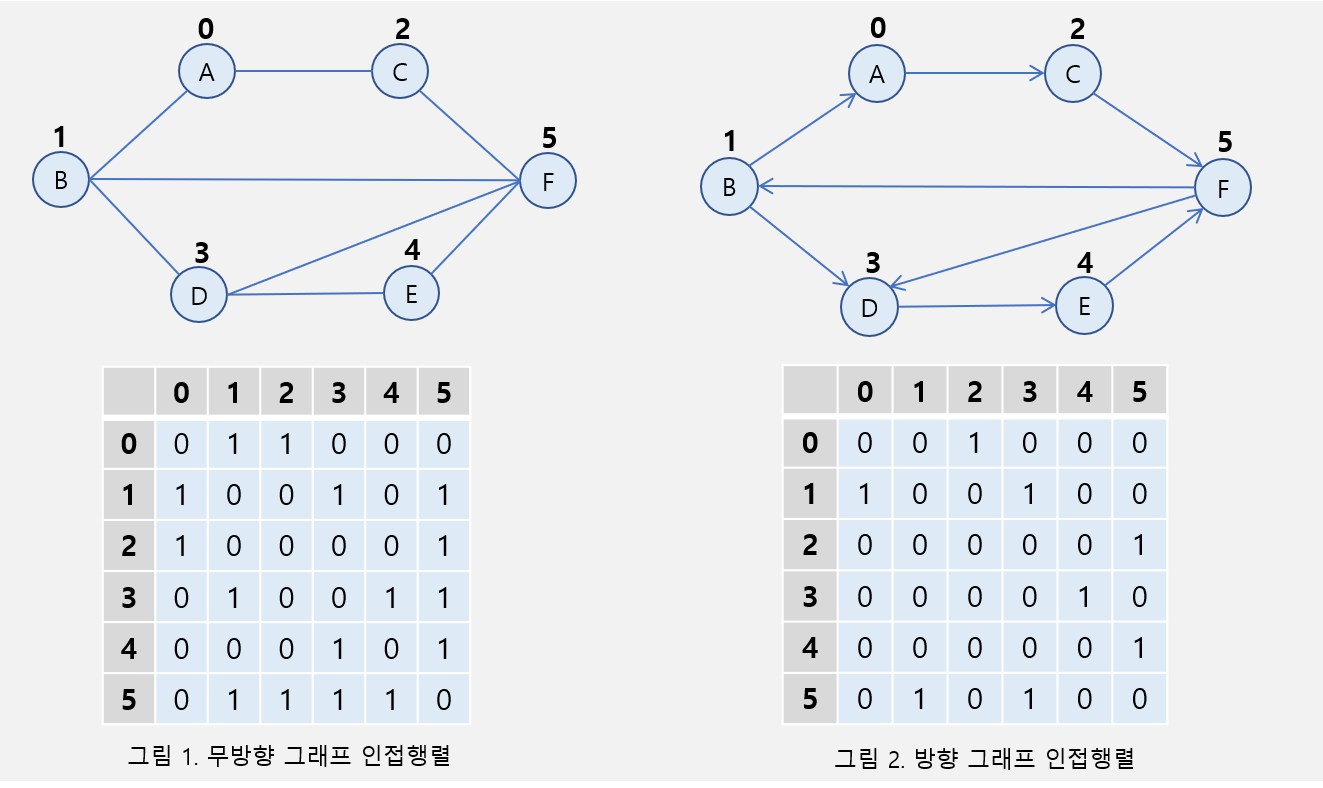
인접 행렬: 노드들의 연결 관계를 나타내는 2차원 리스트
방향 그래프는 엣지를 행 노드에서 열 노드로 나가는지를 기준으로 표기한다.
( ex. (1,0)=1, (0,1)=0 ) 가중치 그래프는 값에 가중치를 넣어주면 된다.

인접 행렬 코드

adjacency_matrix = [[0 for i in range(6)] for i in range(6)]

"""무방향 가중치 없는 그래프"""
adjacency_matrix[0][1] = 1
adjacency_matrix[0][2] = 1
adjacency_matrix[1][5] = 1
adjacency_matrix[1][3] = 1
adjacency_matrix[2][5] = 1
adjacency_matrix[3][4] = 1
adjacency_matrix[3][5] = 1
adjacency_matrix[4][5] = 1

for i in range(len(adjacency_matrix[0])) :
    for j in range(i, len(adjacency_matrix[0])) :
        if i == j :
            adjacency_matrix[i][j] = 0
        else :
            adjacency_matrix[j][i] = adjacency_matrix[i][j]

인접 리스트: 각 노드의 엣지를 리스트에 저장한다.
노드 클래스에 인접 리스트 속성을 추가해 각 노드 별 인접 노드들을 리스트에 저장한다.

인접 리스트 코드

"""인접 리스트 방식을 통해 엣지 구현하기"""
class GraphNode:
  def __init__(self, name):
    self.name = name

    # 인접리스트 속성 추가
    self.adjacent_node = []
    
node1 = GraphNode("A")
node2 = GraphNode("B")
node3 = GraphNode("C")

graph = [node1, node2, node3]

# 인접리스트 속성에 인접한 노드 추가
node1.adjacent_node.append(node2)
node1.adjacent_node.append(node3)

1-5 공간 복잡도와 시간 복잡도

노드 수 : V
엣지 수 : E
- 엣지는 최대(모든 노드가 서로 연결) 무방향 그래프의 경우 \(V^2/2\) 개, 방향 그래프의 경우 \(V^2\) 개까지 있을 수 있다.

노드를 저장하는 공간

노드는 리스트나 딕셔너리에 노드 수만큼 저장한다 => O(V)

엣지를 저장하는 공간

인접 행렬의 경우
- 노드의 수가 V일 때, 인접 행렬의 크기는 V*V => O(\(V^2\))
인접 리스트의 경우
- 노드의 수가 V, 엣지의 수가 E => O(V+E)
- E의 경우 최대(모든 노드가 서로 연결) \(V^2\) 가질 수 있어 O(\(V^2\))로 표기하기도 한다.\

노드가 서로 연결되었는지 확인하는데 걸리는 시간

인접 행렬은 한 번에 접근 => O(1)
인접 리스트는 해당 노드의 인접 리스트 속성을 선형탐색 해야 한다. 최악의 경우(모든 노드와 인접) O(V)만큼 걸릴 수 있다.

2. 그래프 탐색

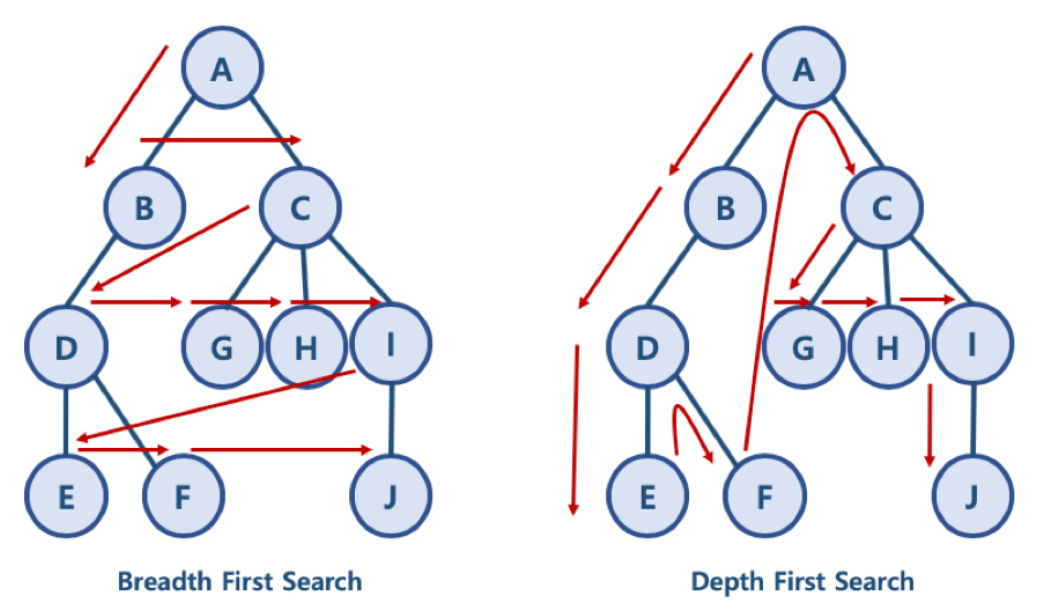
출처: 잔재미코딩

BFS (Breadth First Search)

같은 높이에 있는 노드들을 먼저 탐색한 후 그 다음 높이에 있는 노드들을 탐색하는 방식이다.
(국어, 수학, 영어를 1챕터 끝낸 후, 2챕터, 3챕터… 이렇게 끝내는 방식)

시간 복잡도: O(V+E)

BFS 알고리즘 코드

"""그래프 생성"""
graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
  
"""BFS알고리즘"""
def bfs(graph, start_node):

    # 방문한 노드
    visited = list()

    # 방문해야할 노드 (큐)
    need_visit = list()
      
    # 시작 노드를 방문해야할 노드의 목록 큐에 넣는다
    need_visit.append(start_node)
      
    # 방문해야할 노드가 없을 때까지
    while need_visit :

        # 가장 우선 방문해야할 노드를 하나 꺼낸다 (큐를 쓰는 이유)
        node = need_visit.pop(0)

        # 처음 방문한 노드면
        if node not in visited:

            # 방문 표시
            visited.append(node)

            # 방문해야할 노드의 목록에 방문한 노드의 인접 노드들을 모두 넣는다
            need_visit.extend(graph[node])
    
  return visited
  
"""이 방법은 코드가 간단하지만 방문한 노드들도 계속 다시 방문해야할 노드의 목록으로 들어가게 된다.
물론 if문이 있기 때문에 괜찮지만 비효율적일 수 있다고 생각이든다."""
        

bfs(graph, "A")
-----------------------------------------------------
['A', 'B', 'C', 'D', 'G', 'H', 'I', 'E', 'F', 'J']

DFS (Depth First Search)

각 노드에서 최대한 깊은 높이까지 탐색한 후 그 다음 노드에서 같은 방식으로 탐색하는 방식이다.
(국어를 먼저 끝내고, 수학, 영어 이렇게 하나씩 끝까지 하는 방식)

시간 복잡도: O(V+E)

DFS 알고리즘 코드

"""그래프 생성"""
graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
  
"""DFS알고리즘"""
def dfs(graph, start_v):

  # 방문을 완료한 목록
  visited = []

  # 방문이 필요한 인접 노드
  stack = [start_v]

  # 방문할 노드가 남아 있으면
  while stack:
    v = stack.pop()
    visited.append(v)

    for w in graph[v]:
      if w not in visited:
        stack.append(w)
      
    return visited
        

dfs(graph, "A")
-----------------------------------------------------
['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']

3. 최단 경로 알고리즘

가중치를 고려하지 않는 최단 경로 알고리즘: BFS

기존 BFS알고리즘에 노드 속성에 새로운 속성 predecessor을 추가한다.

BFS 최단 경로 알고리즘 코드

def bfs:
  # 추가 예정

def back_track(destination_node):   
"""최단 경로를 찾기 위한 back tracking 함수"""    
res_str = ""  # 리턴할 결과 문자열    
temp = destination_node  
while temp is not None:       
          res_str = f"{temp.station_name} {res_str}"  
          temp = temp.predecessor
return res_str

가중치를 고려하는 최단 경로 알고리즘: Dijkstra

Twitter Facebook LinkedIn

JaeYeong Kim