[Data_structure] 해시 테이블

March 25, 2021

1. 특징

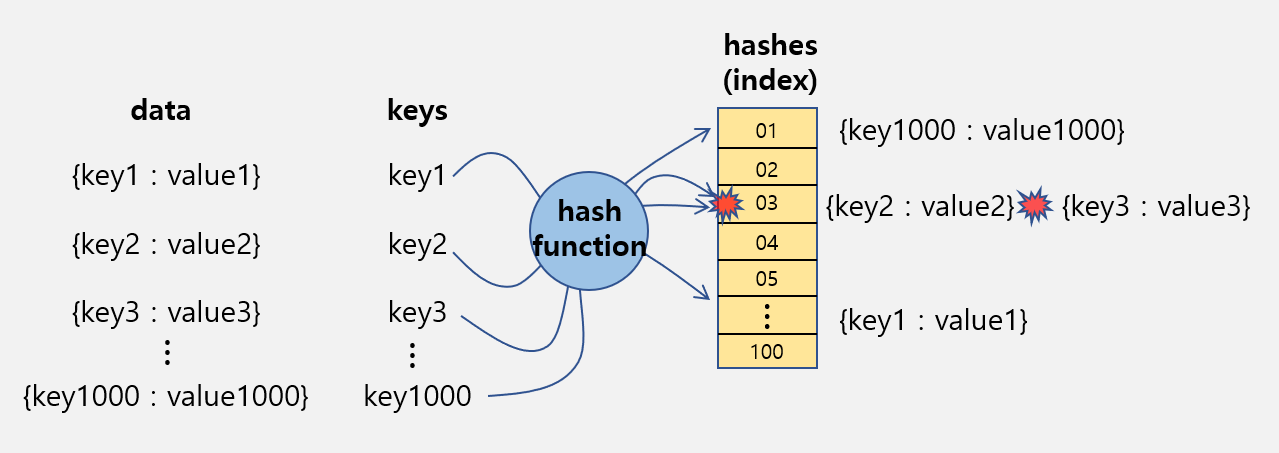
해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(index) 혹은 주소 삼아 데이터의 값(value)을 키와 함께 저장하는 자료구조를 해시테이블(hash table)이라고 합니다.
이 때 데이터가 저장되는 곳을 버킷(bucket) 또는 슬롯(slot)이라고 합니다. 해시테이블의 기본 연산은 삽입, 삭제, 탐색(search)입니다.
해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환(many-to-one 대응)하기 때문에 해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생하게 됩니다.
현재까지 개발된 거의 모든 해시함수는 해시충돌을 일으키는 것으로 확인됐다고 합니다. 물론 해시충돌 자체를 줄이는 것도 의미가 있겠습니다만, 중요한 것은 해시충돌이 해시값 전체에 걸쳐 균등하게 발생하게끔 하는 것입니다.
해시충돌이 발생할 가능성이 있음에도 해시테이블을 쓰는 이유는 적은 리소스로 많은 데이터를 효율적으로 관리하기 위해서입니다.
예컨대 해시함수로 하드디스크나 클라우드에 존재하는 무한에 가까운 데이터(키)들을 유한한 개수의 해시값으로 매핑함으로써 작은 크기의 캐쉬 메모리로도 프로세스를 관리할 수 있게 됩니다.
색인(index)에 해시값을 사용함으로써 모든 데이터를 살피지 않아도 검색과 삽입/삭제를 빠르게 수행할 수 있습니다.
충돌 문제에 대한 해결법은 챕터 3번에서 다루도록 하고, 그 전에 해시함수에 대해 먼저 알아보겠습니다.

2. 해시함수

해시함수(hash function)란 데이터의 효율적 관리를 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수입니다.
이 때 매핑 전 원래 데이터의 값을 키(key), 매핑 후 데이터의 값을 해시값(hash value), 매핑하는 과정 자체를 해싱(hashing)라고 합니다.
해시테이블의 크기가 m이라면, 좋은 해시함수는 임의의 키값을 임의의 해시값에 매핑할 확률이 1/m이 될 겁니다. 다시 말해 특정 값에 치우치지 않고 해시값을 고르게 만들어내는 해시함수가 좋은 해시함수라는 이야기입니다.

division method

나눗셈법은 간단하면서도 빠른 연산이 가능한 해시함수입니다. 숫자로 된 키를 해시테이블 크기 m으로 나눈 나머지를 해시값으로 반환합니다. m은, 대개 소수(prime number)를 쓰며 특히 2의 제곱수와 거리가 먼 소수를 사용하는 것이 좋다고 합니다. 다시 말해 해시함수 특성 때문에 해시테이블 크기가 정해진다는 단점이 있다는 이야기입니다.

multiplication method

숫자로 된 키가 k이고 A는 0과 1 사이의 실수일 때 곱셈법은 다음과 같이 정의됩니다. m이 얼마가 되든 크게 중요하지는 않으며 보통 2의 제곱수로 정한다고 합니다. 나눗셈법보다는 다소 느리다고 합니다. 2진수 연산에 최적화한 컴퓨터 구조를 고려한 해시함수라고 합니다.
h(k)=(kAmod1)×m

universal hasing

다수의 해시함수를 만들고, 이 해시함수의 집합 H에서 무작위로 해시함수를 선택해 해시값을 만드는 기법입니다. H에서 무작위로 뽑은 해시함수가 주어졌을 때 임의의 키값을 임의의 해시값에 매핑할 확률을 1/m로 만드려는 것이 목적입니다. 다음과 같은 특정 조건의 해시함수 집합 H는 1/m으로 만드는 게 가능하다고 수학적으로 증명됐습니다.
해시테이블의 크기 m를 소수로 정한다. 키값을 다음과 같이 r+1개로 쪼갠다 : k0, k1,…, kr 0부터 m−1 사이의 정수 가운데 하나를 무작위로 뽑는다. 분리된 키값의 개수(r+1)만큼 반복해서 뽑는다. 이를 a=[a0,a1,…,ar]로 둔다. 따라서 a의 경우의 수는 모두 mr+1가지이다. 해시함수를 다음과 같이 정의한다 : ha(x)=Σri=0(aikimod m) a가 mr+1가지이므로 해시함수의 집합 H의 요소 수 또한 mr+1개이다. 위와 같은 조건에서는 키가 동일하더라도 a가 얼마든지 랜덤하게 달라질 수 있고, 이에 해당하는 해시함수 ha 또한 상이해지기 때문에 H는 유니버설 함수가 됩니다.

코드

"""나누기 방법"""
def hash_function_remainder(key, array_size):
    return key % array_size

"""곱하기 방법"""
def hash_function_multiplication(key, array_size, a):
    temp = a * key # key를 임의로 정한 값 a와 곱한다
    temp = temp - int(temp) # 소수점 부분만 사용한다 (0~1사이의 값을 얻는다)
    
    return int(array_size * temp) # temp와 배열 크기를 곱한 수의 자연수 부분만 리턴한다 (0~array_size사이의 값을 얻는다)

"""파이썬 내부함수 hash"""

print(hash(15.1234))  # 284541027336970255
print(hash("파이썬"))  # -8002119629611903017

3. 해시값이 충돌하는 경우

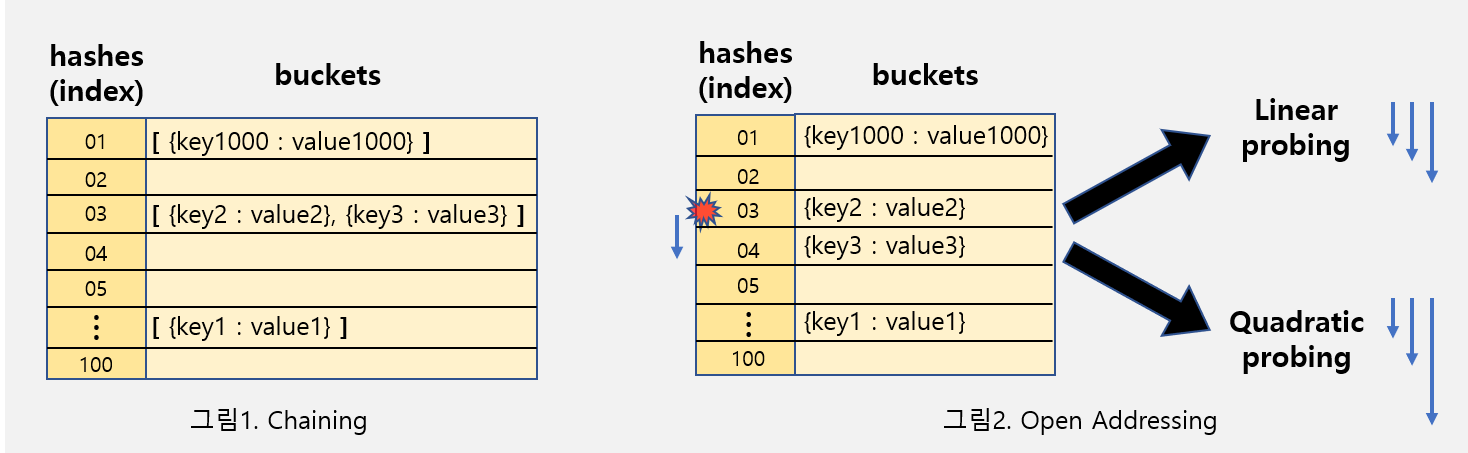
Chaining

해시충돌 문제를 해결하기 위한 간단한 아이디어 가운데 하나는 한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 것입니다. 해당 버킷에 데이터가 이미 있다면 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현(연결리스트)하기 때문에 체인이라는 말이 붙은 것 같습니다. 유연하다는 장점을 가지나 메모리 문제를 야기할 수 있습니다.

코드

# HDLL.py

class Node:
  """링크드 리스트의 노드 클래스"""
  def __init__(self, key, value):
      self.key = key
      self.value = value
      self.next = None  # 다음 노드에 대한 레퍼런스
      self.prev = None  # 전 노드에 대한 레퍼런스


class LinkedList:
    """링크드 리스트 클래스"""
    def __init__(self):
        self.head = None  # 링크드 리스트의 가장 앞 노드
        self.tail = None  # 링크드 리스트의 가장 뒤 노드
          

    def find_node_with_key(self, key):
        """링크드 리스트에서 주어진 데이터를 갖고있는 노드를 리턴한다. 단, 해당 노드가 없으면 None을 리턴한다"""
        iterator = self.head   # 링크드 리스트를 돌기 위해 필요한 노드 변수

        while iterator is not None:
            if iterator.key == key:
                return iterator

            iterator = iterator.next

        return None


    def append(self, key, value):
        """링크드 리스트 추가 연산 메소드"""
        new_node = Node(key, value)

        # 빈 링크드 리스트라면 head와 tail을 새로 만든 노드로 지정
        if self.head is None:
            self.head = new_node
            self.tail = new_node
        # 이미 노드가 있으면
        else:
            self.tail.next = new_node  # 마지막 노드의 다음 노드로 추가
            new_node.prev = self.tail
            self.tail = new_node  # 마지막 노드 업데이


    def delete(self, node_to_delete):
        """더블리 링크드 리스트 삭제 연산 메소드"""

        # 링크드 리스트에서 마지막 남은 데이터를 삭제할 때
        if node_to_delete is self.head and node_to_delete is self.tail:
            self.tail = None
            self.head = None

        # 링크드 리스트 가장 앞 데이터 삭제할 때
        elif node_to_delete is self.head:
            self.head = self.head.next
            self.head.prev = None

        # 링크드 리스트 가장 뒤 데이터 삭제할 떄
        elif node_to_delete is self.tail:
            self.tail = self.tail.prev
            self.tail.next = None

        # 두 노드 사이에 있는 데이터 삭제할 때
        else:
            node_to_delete.prev.next = node_to_delete.next
            node_to_delete.next.prev = node_to_delete.prev

        return node_to_delete.value


    def __str__(self):
        """링크드 리스트를 문자열로 표현해서 리턴하는 메소드"""
        res_str = ""

        # 링크드 리스트 안에 모든 노드를 돌기 위한 변수. 일단 가장 앞 노드로 정의한다.
        iterator = self.head

        # 링크드 리스트 끝까지 돈다
        while iterator is not None:
            # 각 노드의 데이터를 리턴하는 문자열에 더해준다
            res_str += "{}: {}\n".format(iterator.key, iterator.value)
            iterator = iterator.next  # 다음 노드로 넘어간다

        return res_str
  

from HDLL import LinkedList

class HashTable:
    def __init__(self, capacity):
        self._capacity = capacity  # 파이썬 리스트 수용 크기 저장
        self._table = [LinkedList() for _ in range(self._capacity)]  # 파이썬 리스트 인덱스에 반 링크드 리스트 저장

    def _hash_function(self, key):
        """
        주어진 key에 나누기 방법을 사용해서 해시된 값을 리턴하는 메소드
        주의: key는 파이썬 불변 타입이여야 한다.
        """
        return hash(key) % self._capacity


    def _get_linked_list_for_key(self, key):
        """주어진 key에 대응하는 인덱스에 저장된 링크드 리스트를 리턴하는 메소드"""
        hashed_index = self._hash_function(key)

        return self._table[hashed_index]


    def _look_up_node(self, key):
        """파라미터로 받은 key를 갖고 있는 노드를 리턴하는 메소드"""
        linked_list = self._get_linked_list_for_key(key)
        return linked_list.find_node_with_key(key)

    def look_up_value(self, key):
        """
        주어진 key에 해당하는 데이터를 리턴하는 메소드
        """
        return self._look_up_node(key).value

              
    def insert(self, key, value):
        """
        새로운 key - 데이터 쌍을 삽입시켜주는 메소드
        이미 해당 key에 저장된 데이터가 있으면 해당 key에 대응하는 데이터를 바꿔준다
        """
        existing_node = self._look_up_node(key)  # 이미 저장된 key인지 확인한다

        if existing_node is not None:
            existing_node.value = value  # 이미 저장된 key면 데이터만 바꿔주고
        else:
            # 없는 키면 새롭게 삽입시켜준다
            linked_list = self._get_linked_list_for_key(key)
            linked_list.append(key, value)

      def delete_by_key(self, key):
      """주어진 key에 해당하는 key - value 쌍을 삭제하는 메소드"""
      node_to_delete = self._look_up_node(key)  # 이미 저장된 key인지 확인한다

      # 저장되어 있는 key면 삭제한다
      if node_to_delete is not None:
          linked_list = self._get_linked_list_for_key(key)
          linked_list.delete(node_to_delete)

    def __str__(self):
        """해시 테이블 문자열 메소드"""
        res_str = ""

        for linked_list in self._table:
            res_str += str(linked_list)

        return res_str[:-1]

Open Addressing

open addressing은 그 구조상 해시충돌 문제가 발생할 수 있습니다. 앞선 예시에서 살펴봤듯 특정 해시값에 키가 몰리게 되면 open addressing의 효율성이 크게 떨어집니다. 해시충돌은 탐사(probing) 방식으로 해결할 수 있습니다. 탐사란 삽입, 삭제, 탐색을 수행하기 위해 해시테이블 내 새로운 주소(해시값)를 찾는 과정입니다.
선형 탐사(Linear probing) 는 가장 간단한 방식입니다. 앞선 예시에 해당합니다. 최초 해시값에 해당하는 버킷에 다른 데이터가 저장돼 있으면 해당 해시값에서 고정 폭(예컨대 1칸)을 옮겨 다음 해시값에 해당하는 버킷에 액세스(삽입, 삭제, 탐색)합니다. 여기에 데이터가 있으면 고정폭으로 또 옮겨 액세스합니다. 그런데 탐사 이동폭이 고정돼 있는 선형탐사는 특정 해시값 주변 버킷이 모두 채워져 있는 primary clustring 문제에 취약하다고 합니다. 예컨대 아래 그림처럼 52~56까지 데이터가 저장돼 있고 임의의 키의 최초 해시값이 52라면 탐사를 네 번 수행하고 나서야 원하는 위치를 찾을 수 있습니다. 모두 빈 버킷이었다면 단 한 번의 해시만으로도 저장할 수 있었을 텐데 말이죠.

제곱 탐사(Quadratic probing) 는 고정 폭으로 이동하는 선형 탐사와 달리 그 폭이 제곱수로 늘어난다는 특징이 있습니다. 예컨대 임의의 키값에 해당하는 데이터에 액세스할 때 충돌이 일어나면 12칸을 옮깁니다. 여기에서도 충돌이 일어나면 이번엔 22칸, 그 다음엔 32칸 옮기는 식입니다.

하지만 제곱탐사는 여러 개의 서로 다른 키들이 동일한 초기 해시값(아래에서 initial probe)을 갖는 secondary clustering에 취약하다고 합니다. 초기 해시값이 같으면 다음 탐사 위치 또한 동일하기 때문에 효율성이 떨어집니다. 예컨대 아래 그림에서 초기 해시값이 7인 데이터를 삽입해야 할 경우 선형 탐사 기법보다 성큼성큼 이동하더라도 탐사를 네 번 수행하고 나서야 비로소 데이터를 저장할 수 있습니다.

코드

class HashTable(object):

  def __init__(self):
      self.max_length = 8
      self.max_load_factor = 0.75
      self.length = 0
      self.table = [None] * self.max_length

  def __len__(self):
      return self.length

  def __setitem__(self, key, value):
      self.length += 1
      hashed_key = self._hash(key)
      while self.table[hashed_key] is not None:
          if self.table[hashed_key][0] == key:
              self.length -= 1
              break
          hashed_key = self._increment_key(hashed_key)
      tuple = (key, value)
      self.table[hashed_key] = tuple
      if self.length / float(self.max_length) >= self.max_load_factor:
          self._resize()

  def __getitem__(self, key):
      index = self._find_item(key)
      return self.table[index][1]

  def __delitem__(self, key):
      index = self._find_item(key)
      self.table[index] = None

  def _hash(self, key):
      # TODO more robust
      return hash(key) % self.max_length

  def _increment_key(self, key):
      return (key + 1) % self.max_length

  def _find_item(self, key):
      hashed_key = self._hash(key)
      if self.table[hashed_key] is None:
          raise KeyError
      if self.table[hashed_key][0] != key:
          original_key = hashed_key
          while self.table[hashed_key][0] != key:
              hashed_key = self._increment_key(hashed_key)
              if self.table[hashed_key] is None:
                  raise KeyError
              if hashed_key == original_key:
                  raise KeyError
      return hashed_key

  def _resize(self):
      self.max_length *= 2
      self.length = 0
      old_table = self.table
      self.table = [None] * self.max_length
      for tuple in old_table:
          if tuple is not None:
              self[tuple[0]] = tuple[1]

4. 시간 복잡도

Chaining

load factor

해시 테이블 연산들을 분석할 때는 load factor라는 것을 사용합니다. load factor a는 해시 테이블이 사용하는 배열의 크기를 m, 해시 테이블 안에 들어 있는 데이터 쌍 수를 n이라고 할 때, a = n/m 인데요. 그냥 해시 테이블이 얼마나 차있는지를 나타내는 변수입니다.

Open addressing을 할 때 해시 테이블의 연산들을 분석할 때는 load factor는 굉장히 중요한 역할을 합니다. 해시 테이블 안에 배열의 크기보다 많은 key - value 쌍을 저장할 수 없기 때문에 load factor는 항상 1보다 작다고 가정합니다.
결과적으로 얘기하면 Open addressing을 사용하는 해시 테이블에서 평균적으로 탐사를 해야 되는 횟수 (기댓값)은 1/1-a 보다 작습니다.

예를들어, 배열이 총 100 칸이라고 하고 90 개의 key - value 쌍을 저장했다고 합시다. 그럼 load factor a =0.9 인 건데요.

기댓값에 a를 대입하면 10이 나옵니다. 그러니까 빈 인덱스를 찾기 위해서 평균적으로 인덱스 10 개보다 적은 인덱스를 확인해도 된다는 뜻이죠. 사실 load factor 가 0.9도 굉장히 load factor가 큰 거고요. 그러니까 해시 테이블이 반이나 차 있어도 평균적으로 두 개의 인덱스만 확인해봐도 빈칸을 찾을 수 있다는 거죠. 모든 a에 대해서 계산을 하면 성공적으로 원하는 인덱스를 찾는데 봐야 하는 인덱스 수는 평균적으로 O(1)O(1)입니다. 탐사가 평균적으로 O(1)O(1)이 걸리는 거죠.

Open addressing을 사용한 해시 테이블 연산들의 시간 복잡도가 O(n)인 이유는 다른 단계들은 O(1)으로 할 수 있는데 탐사가 최악의 경우 O(n)이 걸리기 때문이었는데요. 방금 봤듯이 탐사는 최악의 경우 O(n)이 걸리지만 평균적으로는 O(1)의 시간이 걸립니다.
그러니까 Open addressing을 사용하든 Chaining을 사용하든 해시 테이블의 모든 연산들을 평균적으로 O(1)로 할 수 있습니다. 굉장히 효율적이죠.

연산	시간 복잡도 (최악)	시간 복잡도 (평균)
탐색	O(n)	O(1)
삽입	O(n)	O(1)
삭제	O(n)	O(1)

Open Addressing

연산	시간 복잡도 (최악)	시간 복잡도 (평균)
탐색	O(n)	O(1)
삽입	O(n)	O(1)
삭제	O(n)	O(1)

Twitter Facebook LinkedIn

JaeYeong Kim

1. 특징

2. 해시함수

division method

multiplication method

universal hasing

3. 해시값이 충돌하는 경우

Chaining

Open Addressing

4. 시간 복잡도

Chaining

load factor

Open Addressing

You May Also Enjoy