1. 링크드 리스트

1-1 싱글 링크드 리스트의 특징

내용

• 메모리의 동적할당을 기반으로 구현된 시퀀스형 자료구조입니다. (메모리를 차지하는 크기의 한계가 없다)

• 
• 
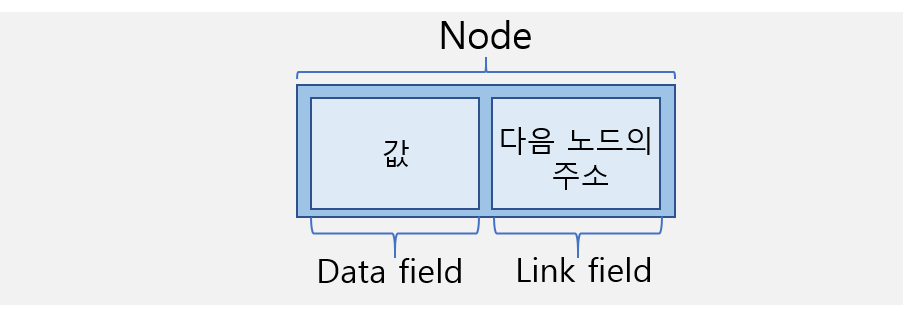
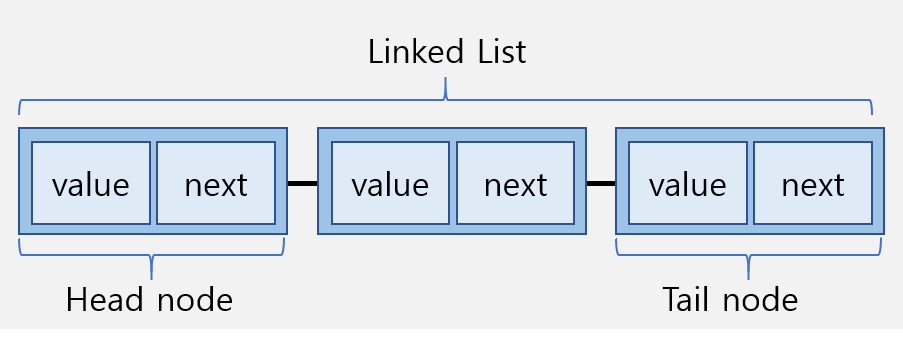
  (C언어에서는 Head에 값을 넣지 않지만 파이썬에서는 그냥 값 갖는다)
• 개별적으로 흩어져 있는 원소의 주소를 연결(Link)하여 하나의 자료구조를 이루고 있다.
• 

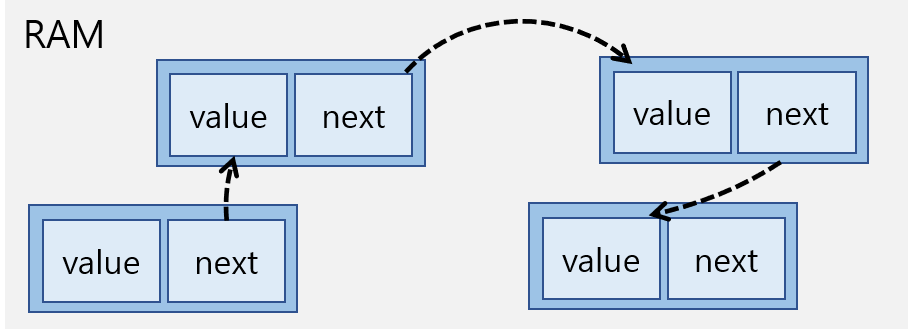
• 임의 접근이 아닌 순차적으로 탐색하며 접근해야 한다. => O(n)

• 이제 노드와 노드간의 연결로 만들어진 링크드 리스트의 객체를 만들 수 있게 해주는 클래스를 작성해 보겠습니다.

  # 노드 클래스
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None
  
  # 링크드 리스트 클래스
  class Linked_List:
    def __init__(self):
      self.head = None
  

1-2 싱글 링크드 리스트 삽입 연산

내용

• 3가지 메소드가 있다
  • 맨 앞에 추가 : prepend
  • 맨 뒤에 추가 : append
  • 특정 노드 뒤에 추가 : insert_after
• 2가지 경우를 고려한다
  • 리스트가 비어있는 경우
  • 리스트에 데이터가 있는 경우

  상황	해결 방법
  리스트가 비어있는 상황	append 또는 prepend에 케이스 추가
  맨 앞에 추가하는 상황	prepend 이용
  맨 뒤에 추가하는 상황	append 이용
  특정 노드 뒤에 추가하는 상황	insert_after 이용

코드

  # 노드 클래스
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None

  # 링크드 리스트 클래스
  class Linked_List:
    def __init__(self):
      self.head = None
      self.tail = None


    """삽입 관련 메소드"""
    # 맨 앞에 추가
    def prepend(self, data):
      new_node = Node(data)
      # 빈 리스트인 상황에 대한 케이스 추가
      if self.head is None:
        self.head = new_node
        self.tail = new_node
      # 비어있지 않은 상황
      else:
        temp = self.head
        self.head = new_node
        new_node.next = temp

    
    # 맨 뒤에 추가
    def append(self, data):
      new_node = Node(data)
      # 빈 리스트인 상황에 대한 케이스 추가
      if self.head is None:
        self.head = new_node
        self.tail = new_node
      # 비어있지 않은 상황
      else:
        self.tail.next = new_node
        self.tail = new_node
    
    # 특정 노드(prev) 뒤에 추가
    def insert_after(self, prev, data):
      new_node = Node(data)
      # 특정 노드(prev)가 tail 노드인 경우
      if self.tail is prev:
        prev.next = new_node
        self.tail = new_node
      else:
        new_node.next = prev.next
        prev.next = new_node

1-3 싱글 링크드 리스트 접근 연산

내용

• 특정 인덱스에 있는 값을 얻고자 할 때 사용되는 연산이다.

코드

  # 노드 클래스
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None

  # 링크드 리스트 클래스
  class Linked_List:
    def __init__(self):
      self.head = None
      self.tail = None

    # 접근 메소드
    def get_node(self, index):
      # head에서 시작
      iter = self.head
      # 인덱스만큼 한 칸씩 이동
      for _ in range(index):
        iter = iter.next
      # 원하는 인덱스에 도착하면 노드 리턴
      return iter

1-4 싱글 링크드 리스트의 탐색 연산

내용

• 특정 값이 있는지 확인하고 싶을 때 사용하는 연산으로 있으면 해당 노드를 리턴한다.

코드

  # 노드 클래스
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None

  # 링크드 리스트 클래스
  class Linked_List:
    def __init__(self):
      self.head = None
      self.tail = None

    # 탐색 메소드
    def get_node(self, data):
      # head에서 시작
      iter = self.head
      # 노드가 있기만 하면 일단 그 노드의 값 탐색
      while iter is not None:
        if iter.data == data:
          return iter

        iter = iter.next
      return None

1-5 싱글 링크드 리스트의 삭제 연산

내용

• 3가지 메소드가 있다
  • 맨 앞 노드 삭제 : pop_left
  • 맨 뒤 노드 삭제 : pop
  • 특정 노드 뒤의 노드 삭제 : delete_after

  상황	해결 방법
  맨 앞 노드 삭제하는 상황	pop_left 이용
  맨 뒤 노드 삭제하는 상황	pop 이용
  특정 노드 뒤의 노드를 삭제하는 상황	delete_after 이용

코드

  # 노드 클래스
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None

  # 링크드 리스트 클래스
  class Linked_List:
    def __init__(self):
      self.head = None
      self.tail = None

    """삭제 메소드"""
    # 맨 앞 노드 삭제
    def pop_left(self):
      self.head = self.head.next
    
    # 맨 뒤 노드 삭제
    def pop(self):
      self.tail = None

    """문제는 새로운 tail을 어떻게 지정해 줄 것인가
    링크드 리스트는 next속성만 있어서 앞의 노드를 가리킬 방법이 없다
    이 문제를 해결할 방법은 2가지가 있다 (제가 생각나는 것 기준)
    1. 처음 노드부터 순차적으로 이동해 끝에 도달하면 그 노드를 tail로 지정한다
    2. 링크드 리스트 객체에 length속성을 만들어 링크드 리스트에 노드를 추가할 때 마다 lenght를 1씩 키운다.
     -> 링크드 리스트 길이에 관한 속성이 생긴다 -> 접근해서 tail로 지정"""

      # 여기서는 다른 코드를 건드리지 않아도 되는 1번 방법 했다
      iter = self.head
      while iter.next is not None:
        iter = iter.next
      self.tail = iter
    
    # 특정 노드 뒤의 노드 삭제
    def delete_after(self, prev):
      if prev.next = self.tail:
        prev.next = None
        self.tail = prev
      else:
        prev.next = prev.next.next

    """내가 원하는 노드를 바로 지정해서 삭제할 수 없는 이유는 그렇게 하면 삭제된 노드의 앞 노드와 뒷 노드를 연결할 수 없기 때문이다.
    그래서 prev(노드)를 지정하게 되면 뒤의 노드를 삭제해도 그 다음 노드와 연결 시켜줄 수 있다."""

    '''다음에 배우게 될 더블리 링크드 리스트는 앞의 노드를 나타내는 prev속성을 가지기 때문에 내가 원하는 노드를 지정해서 삭제할 수 있다.'''
      

2. 더블리 링크드 리스트

2-1 더블리 링크드 리스트의 특징

내용

• 양쪽 방향으로 순회할 수 있도록 구현된 시퀀스형 자료구조입니다.
• 

• 

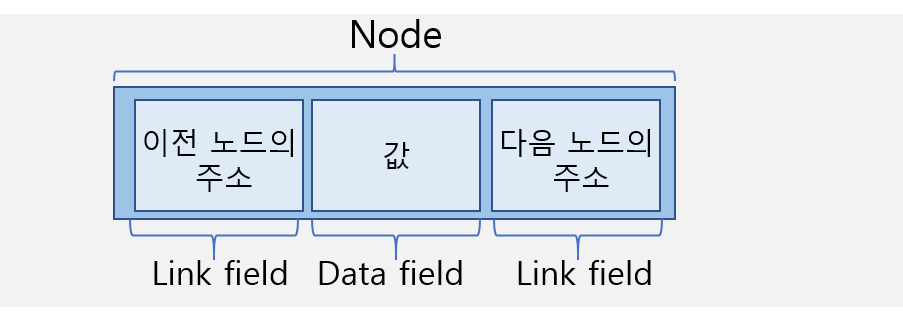
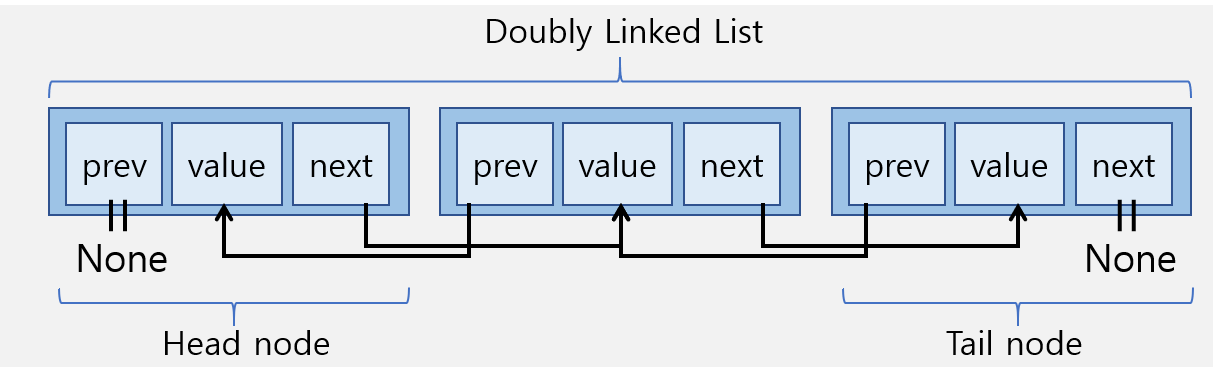
  class Node:
    def __init__(self, data):
      self.data = data
      self.next = None
      self.prev = None
  
  
  class Doubly_Linked_List:
    def __init__(self):
      self.head = None
      self.tail = None
  

• 장점

  연산	장점
  삽입	만약 리스트 길이를 알고 있고 인덱스를 통해 삽입을 한다면 큰 인덱스 값의 경우 끝에서 부터 역으로 순회할 수 있어 시간복잡도 낮출 수 있다
  접근	마찬가지로 리스트 길이를 알고 있고 인덱스를 통해 접근할 때 인덱스 값이 큰 경우 시간복잡도 낮출 수 있다
  탐색	정렬 되어있지 않으면 어차피 선형탐색 해야 하므로 이점이 없어보인다
  삭제	삽입의 경우과 마찬가지로 인덱스를 통해 삭제 한다면 큰 인덱스 값의 경우 끝에서 부터 순회할 수 있어 시간복잡도를 낮출 수 있다

• 단점
  prev라는 새로운 속성을 추가해야 하므로 메모리가 더 사용될 것이다.

2-2 더블리 링크드 리스트 삽입 연산

코드

class Node:
  def __init__(self, data):
    self.data = data
    self.next = None
    self.prev = None


class Doubly_Linked_List:
  def __init__(self):
    self.head = None
    self.tail = None
  
  """삽입 관련 메소드"""

  # 맨 앞에 추가
  def prepend(self, data):
    if self.head is None:
      self.head = new_node
      self.tail = new_node
    else:
      self.head.prev = new_node
      new_node.next = self.head
      self.head = new_node
  
  # 특정 노드 뒤에 추가
  def insert_after(self, prev_node, data):
    new_node = Node(data)
    if prev_node is self.tail:
      prev_node.next = new_node
      new_node.prev = prev_node
      new_node.next = None
      self.tail = new_node
    else:
      new_node.next = prev_node.next
      prev_node.next.prev = new_node
      new_node.prev = prev_node
      prev_node.next = new_node
  

  
  # 맨 뒤에 추가
  def append(self, data):
    new_node = Node(data)
    if self.head is None:
      self.head = new_node
      self.tail = new_node
    else:
      self.tail.next = new_node
      new_node.prev = self.tail
      new_node.next = None
      self.tail = new_node

  """인덱스를 통해 삽입하려는 경우 인자로 받은 인덱스를 메소드 get_node(index)를 사용해 인덱스에 접근해서 new_node를 사이에 넣어준다.
  더블리 링크드 리스트가 아니라 그냥 링크드 리스트면 시간복잡도가 O(n) 이겠지만, 더블리 링크드 리스트는 인덱스가 리스트의 중간을 넘어가면
  끝에서 부터 역순회하도록 함으로써 최대 시간 복잡도를 O(n)/2 로 낮출 수 있다. 근데 O(n/2)도 n이 큰 경우 O(n)으로 생각하기 때문에
  큰 차이는 없을 수도 있다."""

2-3 더블리 링크드 리스트 접근 연산

내용

• 인자로 받은 인덱스와 리스트의 길이를 비교해 length/2 < index 이면 끝에서 부터 역순회 하는게 더 빠르다.
• 리스트의 길이를 알려면 삽입 관련 메소드에 모두 데이터가 추가될 때마다 length 속성에 +1 하도록 코드를 작성해야 한다.
• 접근 메소드에서도 length/2와 index를 비교하는 if문을 추가한다.
• 코드는 생략하겠습니다.

2-4 더블리 링크드 리스트 탐색 연산

내용

• 정렬되어 있지 않다면 어차피 어디 있는지 알 수 없기 때문에 링크드 리스트와 같다.

2-5 더블리 링크드 리스트 삭제 연산

내용

• 삽입과 비슷하게 인덱스를 통해 삭제하려고 한다면 접근에 관한 메소드를 사용해야 하고, 접근 메소드를 위에서 말한 것처럼 작성하면 시간 복잡도를 낮출 수 있다.
• 링크드 리스트에서와 조금 다른 점이 있다. 바로 인자로 내가 삭제하고자 하는 노드를 직접 지정할 수 있다는 것이다.

코드

def delete(self, node_to_delete):
        """더블리 링크드 리스트 삭제 연산 메소드"""
    
        # 링크드 리스트에서 마지막 남은 데이터를 삭제할 때
        if node_to_delete is self.head and node_to_delete is self.tail:
            self.tail = None
            self.head = None
    
        # 링크드 리스트 가장 앞 데이터 삭제할 때
        elif node_to_delete is self.head:
            self.head = self.head.next
            self.head.prev = None
    
        # 링크드 리스트 가장 뒤 데이터 삭제할 떄
        elif node_to_delete is self.tail:
            self.tail = self.tail.prev
            self.tail.next = None
    
        # 두 노드 사이에 있는 데이터 삭제할 때
        else:
            node_to_delete.prev.next = node_to_delete.next
            node_to_delete.next.prev = node_to_delete.prev
    

3. 시간 복잡도

• 접근과 탐색의 경우 싱글과 더블 모두 복잡도는 O(n) 이다.

  연산	시간 복잡도
  접근	O(n)
  탐색	O(n)

• 임의의 위치에 대한 삽입과 삭제의 경우 조금 생각할게 생긴다.
  삽입의 경우 어쨋든 삽입하려는 노드 앞의 노드에 접근해야한다. (prev_node)
  삭제의 경우 싱글은 삽입과 이유가 같다. 앞의 노드에 접근해야 한다. (prev_node)
  삭제의 경우 더블은 바로 해당 노드를 지울 수 있지만 앞 뒤의 노드를 연결(link)해주기 위해서는 결국 접근해야 한다.
  그래서 결론적으로 모두 시간 복잡도는 최악의 경우에 대해 O(n)이다.

  연산	시간 복잡도
  삽입	O(n)
  삭제	O(n)

• 맨 앞/뒤 삽입/삭제의 경우,

  • 삽입의 경우 맨 앞: prepend, 맨 뒤: append는 head와 tail에 바로 접근 (insert_after와 다르게)
  • 삭제의 경우 맨 앞은 싱글, 더블 둘다 바로 삭제하고자 하는 노드(head)에 한 번에 접근 가능,
  • 맨 뒤 삭제의 경우 싱글은 삭제는 한 번에 접근 가능하지만,
    tail 앞의 노드를 새롭게 self.tail로 지정하기 위해 맨 끝 앞의 노드에 접근해야 한다. -> O(n)
  • 맨 뒤 삭제의 경우 더블은 tail에 바로 접근하고 tail앞의 노드 또한 self.tail.prev로 한 번에 접근 가능하다. -> O(1)

  연산	싱글 링크드 리스트	더블리 링크드 리스트
  맨 앞 삽입	O(1)	O(1)
  맨 앞 삭제	O(1)	O(1)
  맨 뒤 삽입	O(1)	O(1)
  맨 뒤 삭제	O(n)	O(1)

4. 결론

• 큐(queue)는 First-In-First-Out 이기 때문에 맨 앞으로만 노드가 삽입되고 삭제되어 싱글 링크드 리스트로 구현해도 된다.

• 스택(stack)은 Last-In-First-Out 이기 때문에 맨 뒤부터 삭제되어 더블리 링크드 리스트로 구현하는게 좋다.

• 파이썬 리스트는 접근이나 탐색의 시간 복잡도가 낮은 동적 배열로 구현된다.