[Data_structure] 트리

March 26, 2021

1. (이진)트리

원소들 간에 계층관계를 가지는 계층적 자료구조이다.
상위 원소에서 하위 원소로 내려가면서 확장되는 Tree모양의 구조이다.
이진트리는 모든 부모노드의 자식노드가 최대 2개만 가지고 있는 트리를 뜻한다.
딕셔너리, 세트, 우선순위 큐와 같은 추상자료형을 구현할 수 있다.
탐색 알고리즘에 많이 사용된다.
(이진)트리의 구성요소

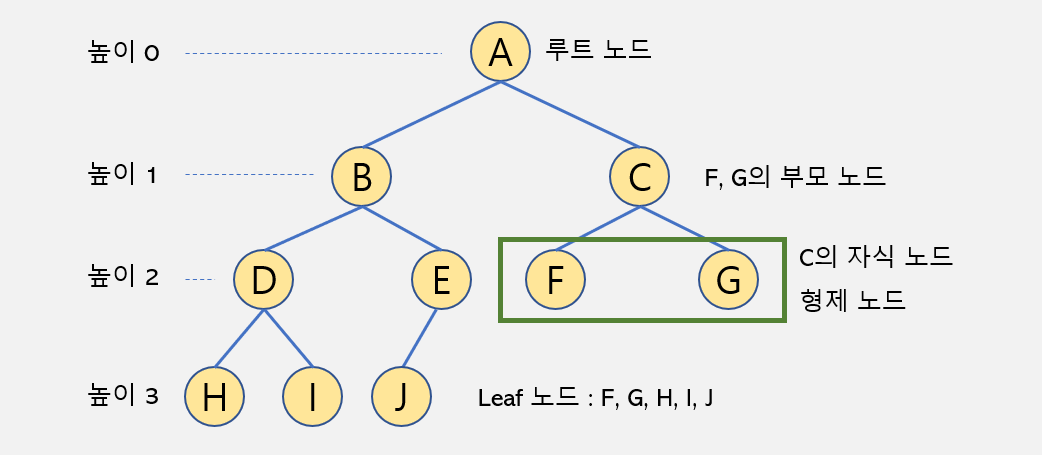
2. 트리의 종류

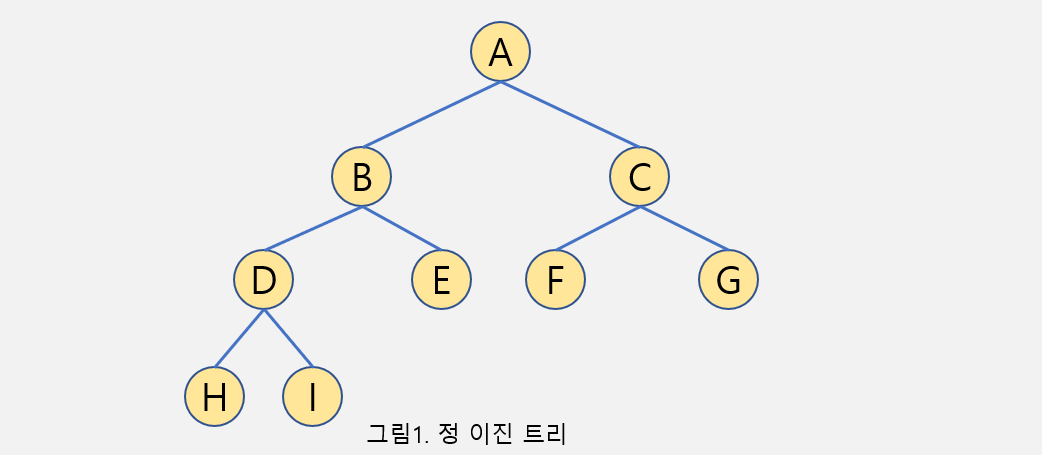
2-1 정 이진 트리 (Full Binary Tree)

자식이 0개이거나 2개인 트리 구조

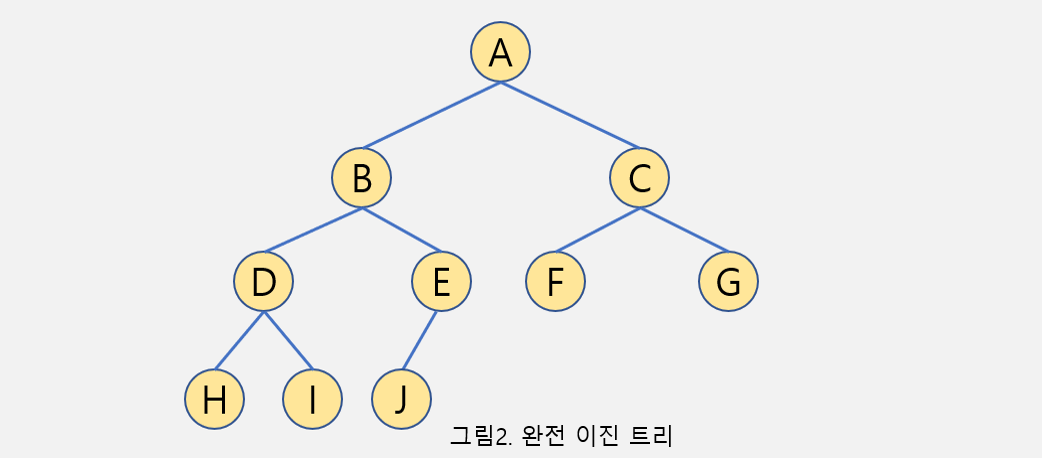
2-2 완전 이진 트리 (Complete Binary Tree) ⭐

마지막 높이 이전까지는 모든 노드들이 채워져 있다.
마지막 높이의 노드는 왼쪽부터 차례대로 채워져 있다.

파이썬 리스트 (동적 배열)로 구현할 수 있습니다.

완전 이진 트리 코드

  
tree = [None, 1, 5, 12, 11, 9, 10, 14, 2, 10] # 트리 그림을 보고 직접 리스트로 작성

def get_parent_index(complete_binary_tree, index):
  """배열로 구현한 완전 이진 트리에서 index번째 노드의 부모 노드의 인덱스를 리턴하는 함수"""
  parent_index = index//2
  if complete_binary_tree[parent_index] != None :
      return parent_index
  else :
      return None


def get_left_child_index(complete_binary_tree, index):
    """배열로 구현한 완전 이진 트리에서 index번째 노드의 왼쪽 자식 노드의 인덱스를 리턴하는 함수"""
    left_child_index = 2*index
    if len(complete_binary_tree) < left_child_index :
        return None
    else:
        return left_child_index


def get_right_child_index(complete_binary_tree, index):
    """배열로 구현한 완전 이진 트리에서 index번째 노드의 오른쪽 자식 노드의 인덱스를 리턴하는 함수"""
    right_child_index = 2*index + 1
    if len(complete_binary_tree) < right_child_index :
        return None
    else :
        return right_child_index

2-3 힙 (Heap) ⭐

완전 이진 트리 구조 + 데이터 값이 힙 속성을 따른다.
- 힙 속성: 모든 노드의 데이터는 자식 노드들의 데이터보다 크다(혹은 작다)
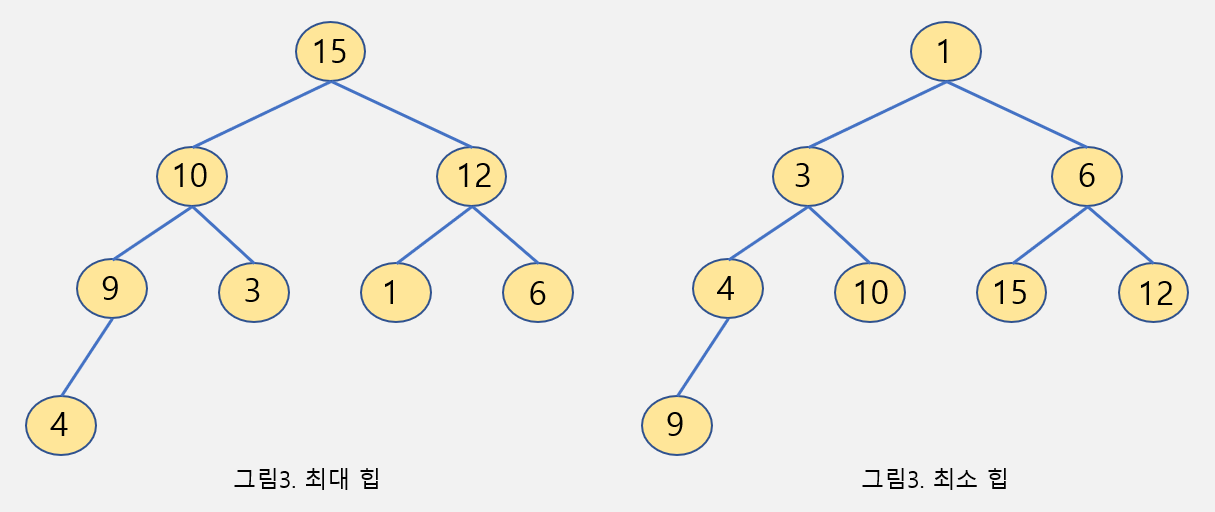
- 최대 힙 은 부모 노드가 자식 노드보다 크도록 트리 구조를 만든다.
- 최소 힙 정렬은 부모 노드가 자식 노드보다 작도록 트리 구조를 만든다.

힙 정렬 에 이용된다.

내림/오름차순 정렬 한다고 했을 때 구현 방법은 다음과 같다.

구현 방법

최대/최소 힙을 만든다.
root와 마지막 노드를 바꿔준다.
(바꾼 노드는 없는 노드 취급한다)
새로운 트리가 힙 속성을 가지도록 heapify를 호출한다.
2-4번을 모든 인덱스를 돌 때까지 반복한다.

🔔 heapify : 파라미터로 넣은 노드를 기준으로 밑에 노드들이 모두 힙 속성을 지키도록 하는 함수

힙 정렬 코드

"""heapify"""

def swap(tree, index_1, index_2):
"""완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다"""
temp = tree[index_1]
tree[index_1] = tree[index_2]
tree[index_2] = temp


def heapify(tree, index, tree_size):
    """heapify 함수"""

    # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
    left_child_index = 2 * index
    right_child_index = 2 * index + 1

    largest = index  # 일단 부모 노드의 값이 가장 크다고 설정

    # 왼쪽 자식 노드의 값과 비교
    if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]:
        largest = left_child_index

    # 오른쪽 자식 노드의 값과 비교
    if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]:
        largest = right_child_index
        
    if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면
        swap(tree, index, largest)  # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔준다
        return heapify(tree, largest, tree_size)  # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다
    #max_value_index = tree.index(max(tree[index], tree[left_child_index], tree[right_child_index]))

"""힙 정렬"""
def heapsort(tree):
"""힙 정렬 함수"""
tree_size = len(tree)

# 마지막 인덱스부터 처음 인덱스까지 heapify를 호출한다 
for index in range(tree_size, 0, -1):
    heapify(tree, index, tree_size)

# 마지막 인덱스부터 처음 인덱스까지
for i in range(tree_size-1, 0, -1):
    swap(tree, 1, i)  # root 노드와 마지막 인덱스를 바꿔준 후
    heapify(tree, 1, i)  # root 노드에 heapify를 호출한다

정렬 알고리즘	시간 복잡도
선택 정렬	O(\(n^2\))
삽입 정렬	O(\(n^2\))
합병 정렬	O(nlg(n))
퀵 정렬	평균 O(nlg(n)) 최악 O(\(n^2\))
힙 정렬	O(nlg(n))

우선 순위 큐 를 구현하는데 이용된다.

값이 큰/작은 순서대로 추출된다.
구현하는 방법은 다음과 같다.
구현 방법
- 값을 삽입하는 연산을 구현한다.
  1. 맨 끝에 노드를 추가한다.
  2. 추가된 노드와 그 부모 노드를 비교해 힙속성을 어기지 않을때까지 바꿔준다.
- 값을 추출하는 연산을 구현한다.
  1. root와 마지막 노드를 바꿔준다. (root노드의 값이 가장 우선순위가 높은 값)
  2. 끝으로 온 노드를 트리에서 빼고 리턴해준다.
  3. root로 온 노드가 힙 속성을 유지하도록 heapify를 호출한다.
  🔔 heapify : 파라미터로 넣은 노드를 기준으로 밑에 노드들이 모두 힙 속성을 지키도록 하는 함수

트리가 힙 속성을 계속 유지하도록 하면서 삽입 추출 연산을 구현하면 우선 순위 큐로 사용할 수 있다.

우선 순위 큐 코드

    
def swap(tree, index_1, index_2):
    """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다"""
    temp = tree[index_1]
    tree[index_1] = tree[index_2]
    tree[index_2] = temp


def heapify(tree, index, tree_size):
    """heapify 함수"""

    # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
    left_child_index = 2 * index
    right_child_index = 2 * index + 1

    largest = index  # 일단 부모 노드의 값이 가장 크다고 설정

    # 왼쪽 자식 노드의 값과 비교
    if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]:
        largest = left_child_index

    # 오른쪽 자식 노드의 값과 비교
    if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]:
        largest = right_child_index
        
    if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면
        swap(tree, index, largest)  # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔준다
        heapify(tree, largest, tree_size)  # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다


def reverse_heapify(tree, index):
    """삽입된 노드를 힙 속성을 지키는 위치로 이동시키는 함수"""
    parent_index = index // 2  # 삽입된 노드의 부모 노드의 인덱스 계산

    # 부모 노드가 존재하고, 부모 노드의 값이 삽입된 노드의 값보다 작을 때
    if 0 < parent_index < len(tree) and tree[index] > tree[parent_index]:
        swap(tree, index, parent_index)  # 부모 노드와 삽입된 노드의 위치 교환
        reverse_heapify(tree, parent_index)  # 삽입된 노드를 대상으로 다시 reverse_heapify 호출        


class PriorityQueue:
    """힙으로 구현한 우선순위 큐"""
    def __init__(self):
        self.heap = [None]  # 파이썬 리스트로 구현한 힙

    def insert(self, data):
        """삽입 메소드"""
        self.heap.append(data)  # 힙의 마지막에 데이터 추가
        reverse_heapify(self.heap, len(self.heap)-1) # 삽입된 노드(추가된 데이터)의 위치를 재배치

    def extract_max(self):
        """최고 우선순위 데이터 추출 메소드"""
        swap(self.heap, 1, len(self.heap) - 1)  # root 노드와 마지막 노드의 위치 바꿈
        max_value = self.heap.pop()  # 힙에서 마지막 노드 추출(삭제)해서 변수에 저장
        heapify(self.heap, 1, len(self.heap))  # 새로운 root 노드를 대상으로 heapify 호출해서 힙 속성 유지
        return max_value  # 최우선순위 데이터 리턴

    def __str__(self):
        return str(self.heap)
    

연산	정렬된 동적 배열	정렬된 링크드 리스트	힙
삽입	O(n)	O(n)	O(lg(n))
추출	O(1)	O(1)	O(lg(n))

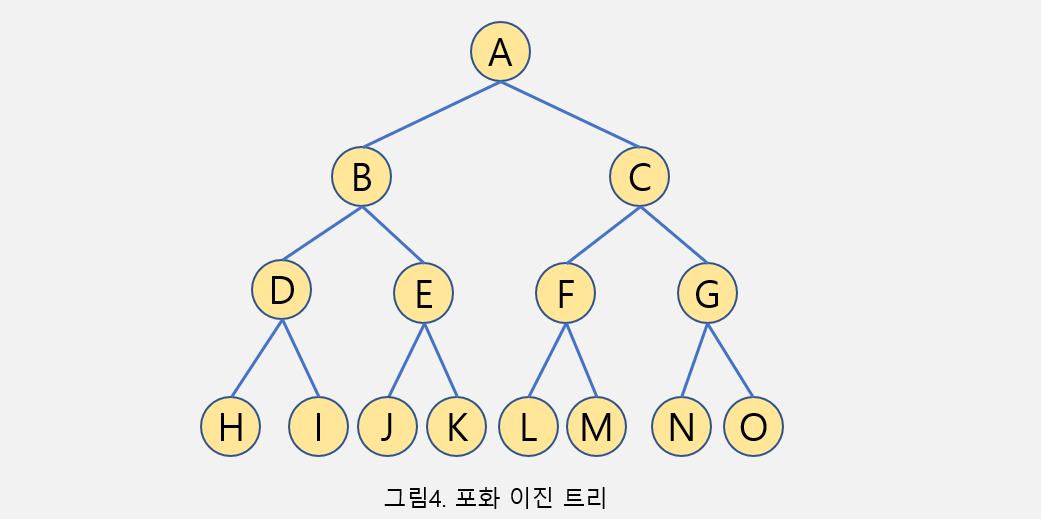
2-4 포화 이진 트리 (Perfect Binary Tree)

모든 높이에서 노드가 채워진 트리 구조

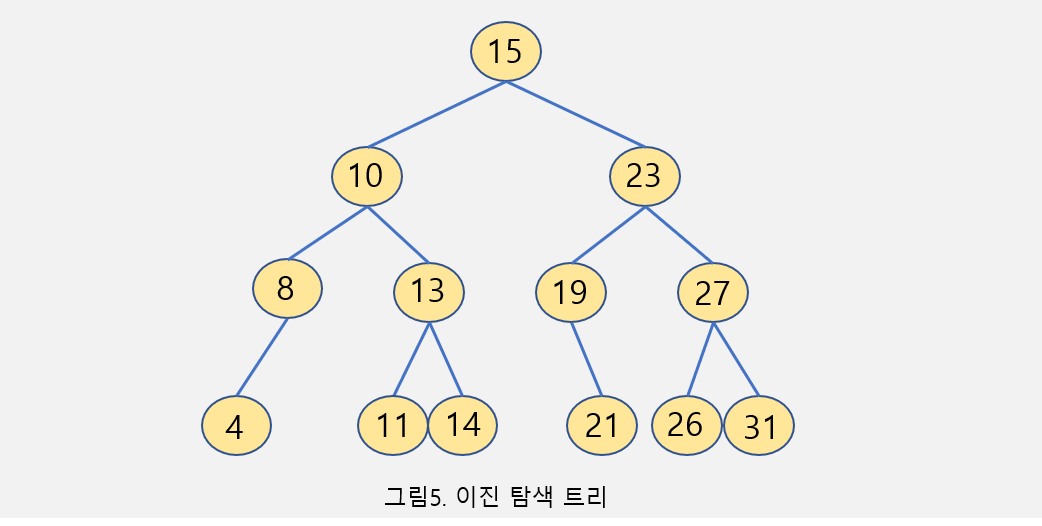
2-5 이진 탐색 트리 (Binary Search Tree) ⭐

임의의 노드를 기준으로 왼쪽 자식 노드는 더 작고 오른쪽 자식 노드는 더 크도록 정렬 되어 있는 자료 구조
딕셔너리 또는 세트를 구현할 때 사용된다. 하지만 해시 테이블 보다 탐색, 삽입, 삭제 연산의 시간 복잡도가 더 크다.
정렬이 필요한 딕셔너리, 세트를 구현할 때 이용된다.

탐색/삽입/삭제 코드 구현

이진 탐색 트리 연산 코드

class BinarySearchTree:
  """이진 탐색 트리 클래스"""
  def __init__(self):
      self.root = None

  
  """탐색 연산"""
  def search(self, data):
    """이진 탐색 트리 탐색 메소드, 찾는 데이터를 갖는 노드가 없으면 None을 리턴한다"""
    temp = self.root  # 탐색용 변수, root 노드로 초기화

    # 원하는 데이터를 갖는 노드를 찾을 때까지 돈다
    while temp is not None:
        # 원하는 데이터를 갖는 노드를 찾으면 리턴
        if data == temp.data:
            return temp
        # 원하는 데이터가 노드의 데이터보다 크면 오른쪽 자식 노드로 간다
        if data > temp.data:
            temp = temp.right_child
        # 원하는 데이터가 노드의 데이터보다 작으면 왼쪽 자식 노드로 간다
        else:
            temp = temp.left_child

    return None # 원하는 데이터가 트리에 없으면 None 리턴

    
  """ 삽입 연산"""
  def insert(self, data):
      """이진 탐색 트리 삽입 메소드"""
      new_node = Node(data)  # 삽입할 데이터를 갖는 노드 생성

      # 트리가 비었으면 새로운 노드를 root 노드로 만든다
      if self.root is None:
          self.root = new_node
          return

      temp = self.root  # 저장하려는 위치를 찾기 위해 사용할 변수. root 노드로 초기화한다

      # 원하는 위치를 찾아간다
      while temp is not None:
          if data > temp.data:  # 삽입하려는 데이터가 현재 노드 데이터보다 크다면
              # 오른쪽 자식이 없으면 새로운 노드를 현재 노드 오른쪽 자식으로 만듦
              if temp.right_child is None:
                  new_node.parent = temp
                  temp.right_child = new_node
                  return
              # 오른쪽 자식이 있으면 오른쪽 자식으로 간다
              else:
                  temp = temp.right_child
          else:  # 삽입하려는 데이터가 현재 노드 데이터보다 작다면
              # 왼쪽 자식이 없으면 새로운 노드를 현재 노드 왼쪽 자식으로 만듦
              if temp.left_child is None:
                  new_node.parent = temp
                  temp.left_child = new_node
                  return
              # 왼쪽 자식이 있다면 왼쪽 자식으로 간다
              else:
                  temp = temp.left_child


  @staticmethod
  def find_min(node):
      """(부분)이진 탐색 트리의 가장 작은 노드 리턴"""
      # 코드를 쓰세요
      temp = node  # 탐색 변수. 파라미터 node로 초기화

      # temp가 node를 뿌리로 갖는 부분 트리에서 가장 작은 노드일 때까지 왼쪽 자식 노드로 간다
      while temp.left_child is not None:
          temp = temp.left_child      

      return temp  


  """삭제 연산"""
  def delete(self, data):
      """이진 탐색 트리 삭제 메소드"""
      node_to_delete = self.search(data)  # 삭제할 노드를 가지고 온다
      parent_node = node_to_delete.parent  # 삭제할 노드의 부모 노드

      # 경우 1: 지우려는 노드가 leaf 노드일 때
      if node_to_delete.left_child is None and node_to_delete.right_child is None:
          if self.root is node_to_delete:
              self.root = None
          else:  # 일반적인 경우
              if node_to_delete is parent_node.left_child: 
                  parent_node.left_child = None
              else:
                  parent_node.right_child = None

      # 경우 2: 지우려는 노드가 자식이 하나인 노드일 때:
      elif node_to_delete.left_child is None:  # 지우려는 노드가 오른쪽 자식만 있을 때:
          # 지우려는 노드가 root 노드일 때
          if node_to_delete is self.root:
              self.root = node_to_delete.right_child
              self.root.parent = None
          # 지우려는 노드가 부모의 왼쪽 자식일 때
          elif node_to_delete is parent_node.left_child:
              parent_node.left_child = node_to_delete.right_child
              node_to_delete.right_child.parent = parent_node
          # 지우려는 노드가 부모의 오른쪽 자식일 때
          else:
              parent_node.right_child = node_to_delete.right_child
              node_to_delete.right_child.parent = parent_node

      elif node_to_delete.right_child is None:  # 지우려는 노드가 왼쪽 자식만 있을 때:
          # 지우려는 노드가 root 노드일 때
          if node_to_delete is self.root:
              self.root = node_to_delete.left_child
              self.root.parent = None
          # 지우려는 노드가 부모의 왼쪽 자식일 때
          elif node_to_delete is parent_node.left_child:
              parent_node.left_child = node_to_delete.left_child
              node_to_delete.left_child.parent = parent_node
          # 지우려는 노드가 부모의 오른쪽 자식일 때
          else:
              parent_node.right_child = node_to_delete.left_child
              node_to_delete.left_child.parent = parent_node

      # 경우 3: 지우려는 노드가 2개의 자식이 있을 때
      else:
          successor = self.find_min(node_to_delete.right_child)  # 삭제하려는 노드의 successor 노드 받아오기

          node_to_delete.data = successor.data  # 삭제하려는 노드의 데이터에 successor의 데이터 저장

          # successor 노드 트리에서 삭제
          if successor is successor.parent.left_child:  # successor 노드가 오른쪽 자식일 때
              successor.parent.left_child = successor.right_child
          else:  # successor 노드가 왼쪽 자식일 때
              successor.parent.right_child = successor.right_child        
        
          if successor.right_child is not None:  # successor 노드가 오른쪽 자식이 있을 떄
              successor.right_child.parent = successor.parent
  

평균적으로 이진 탐색 트리의 높이 h는 O(lg(n))이다.

연산	해시 테이블	이진 탐색 트리
탐색	O(h) (평균적 O(lg(n)), 최악 O(n)	평균적 O(1), 최악 O(n)
삽입	O(h) (평균적 O(lg(n)), 최악 O(n)	평균적 O(1), 최악 O(n)
삭제	O(h) (평균적 O(lg(n)), 최악 O(n)	평균적 O(1), 최악 O(n)

3. 결론

Twitter Facebook LinkedIn

JaeYeong Kim