1. 그래디언트 소실과 폭주 문제(vanishing/exploding gradient)
가중치 초기화
역전파 알고리즘은 출력층에서 입력층으로 오차 그래디언트를 전파하면서 진행됩니다. 그런데 알고리즘이 하위층으로 진행될수록 그래디언트가 작아지는 경우가 많습니다. 이 문제를 그래디언트 소실이라고 합니다. 어떤 경우엔 반대로 그래디언트가 점점 커져 여러 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산합니다. 이 문제를 그래디언트 폭주라고 하며 순환 신경망에서 주로 나타납니다. 일반적으로 불안정한 그래디언트는 심층 신경망 훈련을 어렵게 만듭니다. 층마다 학습 속도가 달라질 수 있기 때문입니다.
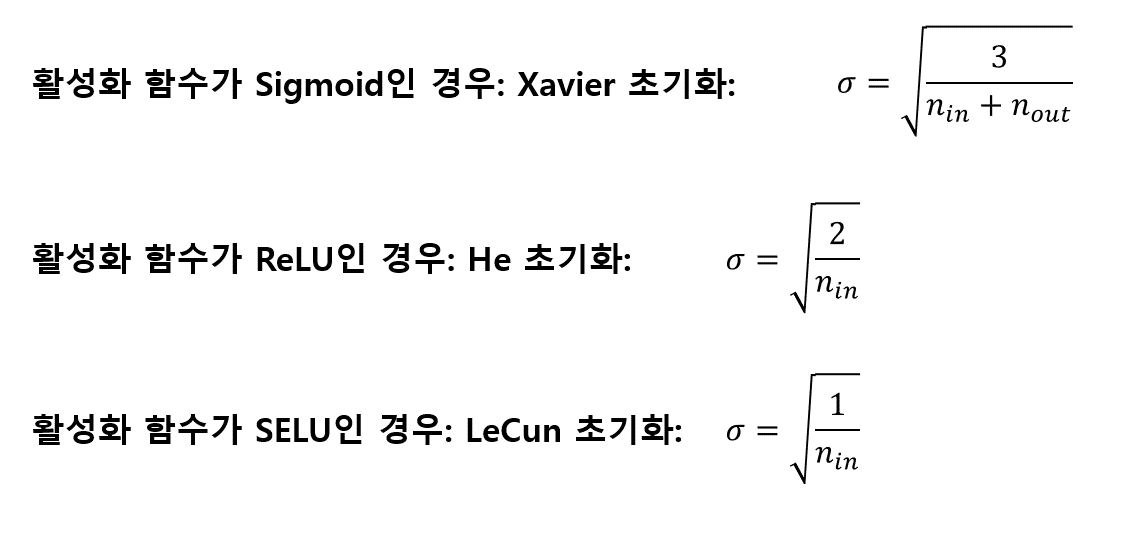
케라스는 기본적으로 균등분포의 글로럿 초기화를 사용합니다. 이를 He 정규분포 형태로 바꾸고 싶으면 다음과 같이 해당하는 층의 kernel_initializer매개변수의 값을 바꾸어 주면 됩니다.
keras.layers.Dense(10, activation='relu', kernel_initializer='he_nomral')
만약 좀 더 세밀하게 튜닝을 원할 경우, 예를 들어 n_in 대신 n_avg 기반의 정규분포 He 초기화를 사용하고 싶다면 다음과 같이 VarianceScaling을 사용할 수 있습니다.
he_avg_init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg', distribution='normal')
keras.layers.Dense(10, activation='sigmoid', kernel_initializer=he_avg_init)
배치 정규화
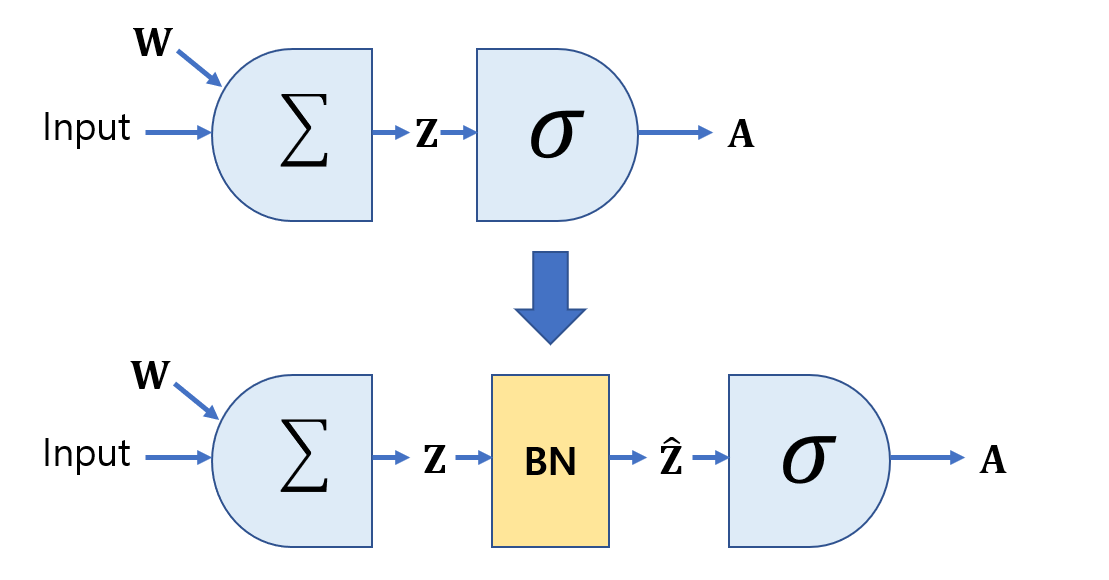
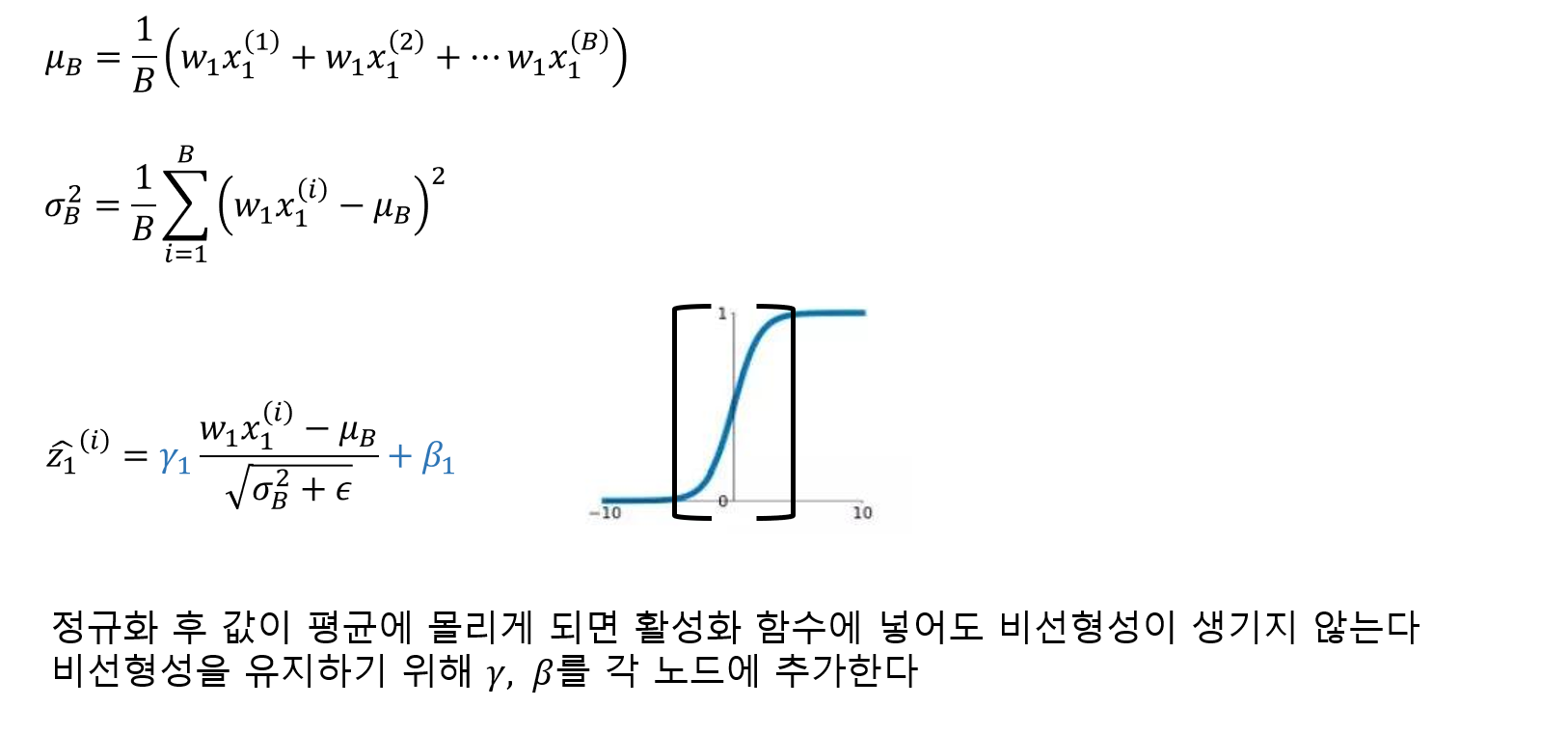
배치 정규화는 각 층에서 활성화 함수를 통과하기 전이나 후에 입력을 정규화한 다음, 두 개의 새로운 파라미터(𝛾, 𝛽)로 결과값의 스케일을 조정하고 이동시킵니다. 정규화 하기 위해서는 평균과 표준편차를 구해야 합니다. 이를 위해 현재 미니배치에서 입력의 평균과 표준편차를 평가합니다. 테스트 시에는 어떻게 할까요? 간단한 문제는 아닙니다. 아마 샘플의 배치가 아니라 샘플 하나에 대한 예측을 만들어야 합니다. 이 경우 입력의 평균과 표준편차를 계산할 방법이 없습니다. 샘플의 배치를 사용한다 하더라도 매우 작거나 독립 동일 분포(IID)조건을 만족하지 못할 수도 있습니다.
케라스에서는 이를 층의 입력 평균과 표준편차의 이동 평균(moving average)을 사용해 훈련하는 동안 최종 통계를 추정함으로써 해결합니다. 케라스의 BatchNormalization층은 이를 자동으로 수행합니다.
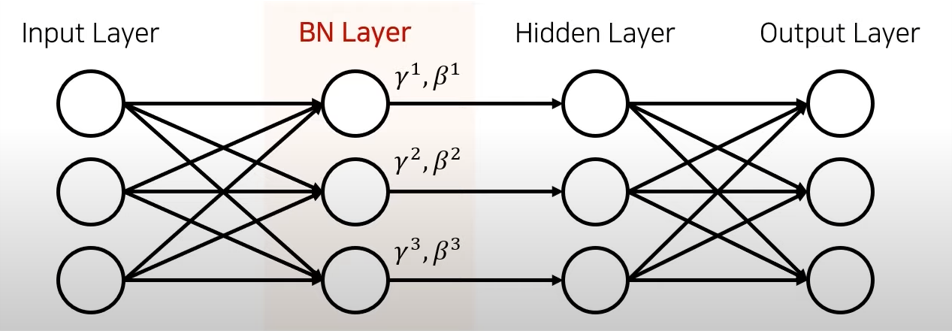
정리하면 배치 정규화 층마다 네 개의 파라미터 벡터가 학습됩니다. 𝛾(출력 스케일 벡터)와 𝛽(출력 이동 벡터)는 일반적인 역전파를 통해 학습됩니다. 𝜇(최종 입력 평균 벡터)와 𝜎(최종 입력 표준편차 벡터)는 지수 이동 평균을 사용하여 추정됩니다. 𝜇와 𝜎는 훈련하는 동안 추정되지만 훈련이 끝난 후에 사용됩니다.(배치 입력 평균과 표준편차를 대체하기 위해)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
>>> model.summary()
-----------------------------------------------------------------
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_4 (Flatten) (None, 784) 0
_________________________________________________________________
batch_normalization (BatchNo (None, 784) 3136
_________________________________________________________________
dense_212 (Dense) (None, 300) 235500
_________________________________________________________________
batch_normalization_1 (Batch (None, 300) 1200
_________________________________________________________________
dense_213 (Dense) (None, 100) 30100
_________________________________________________________________
batch_normalization_2 (Batch (None, 100) 400
_________________________________________________________________
dense_214 (Dense) (None, 10) 1010
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
_________________________________________________________________
배치 정규화 논문의 저자들은 활성화 함수 이후보다 이전에 배치 정규화 층을 추가하는 것이 좋다고 조언합니다. 하지만 작업에 따라 선호되는 방식이 달라 논란이 조금 있습니다. 따라서 두 가지 모두 실험해보고 어떤 것이 더 잘 맞는지 확인하는 것이 좋습니다. 따라서 만약에 활성화 함수 전에 배치 정규화 층을 추가하려면 코드를 다음과 같이 작성해야 합니다. 참고로 배치 정규화 층은 입력마다 이동 파라미터를 포함하므로 편향을 뺄 수 있습니다.(use_bias=False)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(10, activation="softmax")
])
2. 고속 옵티마이저
심층 신경망의 훈련 속도는 심각하게 느릴 수 있습니다. 앞에서 살펴 본 가중치 초기화, 배치 정규화 그리고 좋은 활성함수를 선택하고, 사전 훈련된 네트워크를 재사용하게 되면 훈련 속도를 개선할 수 있습니다. 그리고 또 다른 방법으로 고속 옵티마이저가 있습니다.
그래디언트 모멘텀
모멘텀 최적화는 이전 그래디언트가 얼마였는지를 상당히 중요하게 생각합니다. 다시 말해 그래디언트를 속도가 아니라 가속도로 사용합니다. 이는 기존 경사 하강법보다 더 빠르게 평평한 지역을 탈출하게 도와줍니다. 경사 하강법이 가파른 경사를 꽤 빠르게 내려가지만 좁고 긴 골짜기에서는 오랜 시간이 걸립니다. 반면에 모멘텀 최적화는 골짜기를 따라 최적점에 도달할 때 까지 더 빠르게 내려갑니다.

optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
# 네스테로프 가속 경사
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
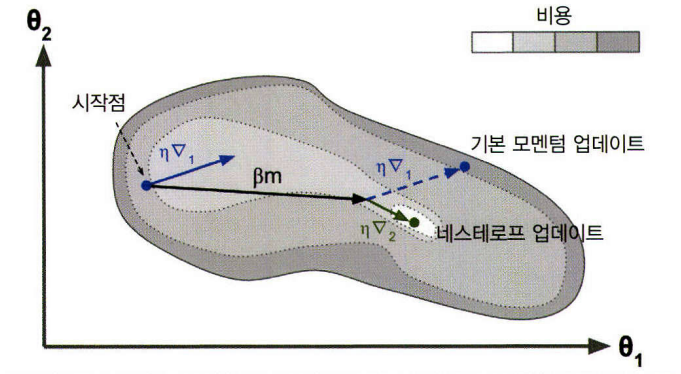
(출처: 핸즈온 머신러닝 2판)
적응적 학습률
가중치 업데이트의 척도가 되는 학습률을 각 가중치의 학습 진행 정도에 따라 다르게 바꿔주는 것을 적응적 학습률이라고 한다.
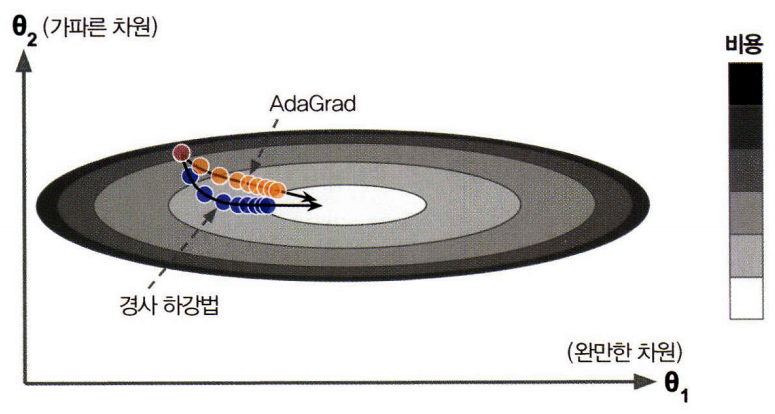
(출처: 핸즈온 머신러닝 2판)

# Adagrad 옵티마이저 (심층 신경망에서는 학습률이 너무 감소되어 최적점에 도착하기 전에 멈추게 된다)
optimizer = keras.optimizers.Adagrad(lr=0.001)
# RMSprop 옵티마이저
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
# Adam 옵티마이저
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
# Adamax 옵티마이저
optimizer = keras.optimizers.Adamax(lr=0.001, beta_1=0.9, beta_2=0.999)
# Nadam 옵티마이저
optimizer = keras.optimizers.Nadam(lr=0.001, beta_1=0.9, beta_2=0.999)
3. 규제
L1, L2
layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
일반적으로 네트워크의 모든 은닉층에 동일한 활성화 함수, 동일한 초기화 전략, 동일한 규제를 적용하기 때문에 반복문을 사용하거나 파이썬의 functools.partial()함수를 사용해 기본 매개변수 값을 사용하여 함수 호출을 감싸 코드의 반복을 피할 수 있습니다.
from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation="softmax")
])
조기 멈춤
from copy import deepcopy
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # 중지된 곳에서 다시 시작합니다
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = deepcopy(sgd_reg)
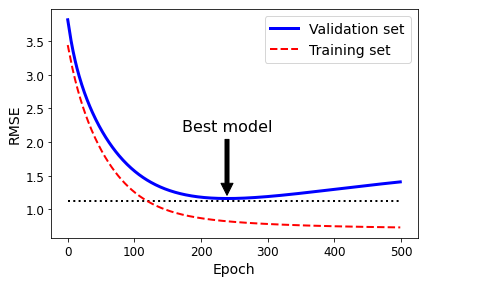
>>> best_epoch, best_model
------------------------------------
(239,
SGDRegressor(eta0=0.0005, learning_rate='constant', max_iter=1, penalty=None,
random_state=42, tol=-inf, warm_start=True))
드롭아웃
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
