CNN의 기초
CNN의 발단
그동안 앞에서 설명한 신경망은 모두 기본 전제가 노드가 서로 완전 연결되어 있는 경우였습니다. 이를 완전 연결층(Fully connected layer)라고 합니다. 이는 목적한 바를 잘 이룰 수 있도록 특징 공간 갖는 모델을 만들 수 있지만, 가중치가 너무 많아 복잡도가 너무 높습니다. 이는 모델의 학습 속도를 더디게 하며 또한 과잉적합에 빠질 가능성을 높이게 됩니다. 컨볼루션 신경망(CNN)은 부분 연결 구조로 이러한 문제를 잘 해결하며 또한 특징을 잘 추출하도록 해줍니다. 이러한 이유로 CNN은 이미지, 비전 분야에서 매우 뛰어난 성능을 발휘했으며, 음성인식이나 자연어 처리같은 다른 작업에도 사용됩니다.
실제로 1958년에 데이비드 허블의 연구에서는 인간의 시각 뉴런은 부분연결 구조를 가진다는 사실을 밝혀냈습니다. 이를 조금 더 자세히 설명하면, 눈의 시각 피질 안의 많은 뉴런은 작은 국부 수용장(Local receptive field)를 가지며 이는 시야의 영역에서 작은 특정 패턴에 뉴런이 반응한다는 것입니다. 예를 들어,
눈이 처음 무언가를 봤을 때는 국부 수용장에 해당하는 작은 영역이 가지는 패턴에 먼저 반응을 하고, 시각 신호가 연속적으로 뇌의 뉴런들을 통과하며 다음 뉴런들은 점점 더 큰 수용장에 있는 복잡한 패턴에 반응을 합니다. 이러한 점에서 CNN은 사람의 눈과 비슷한 원리를 가지고 있다고 할 수 있습니다.
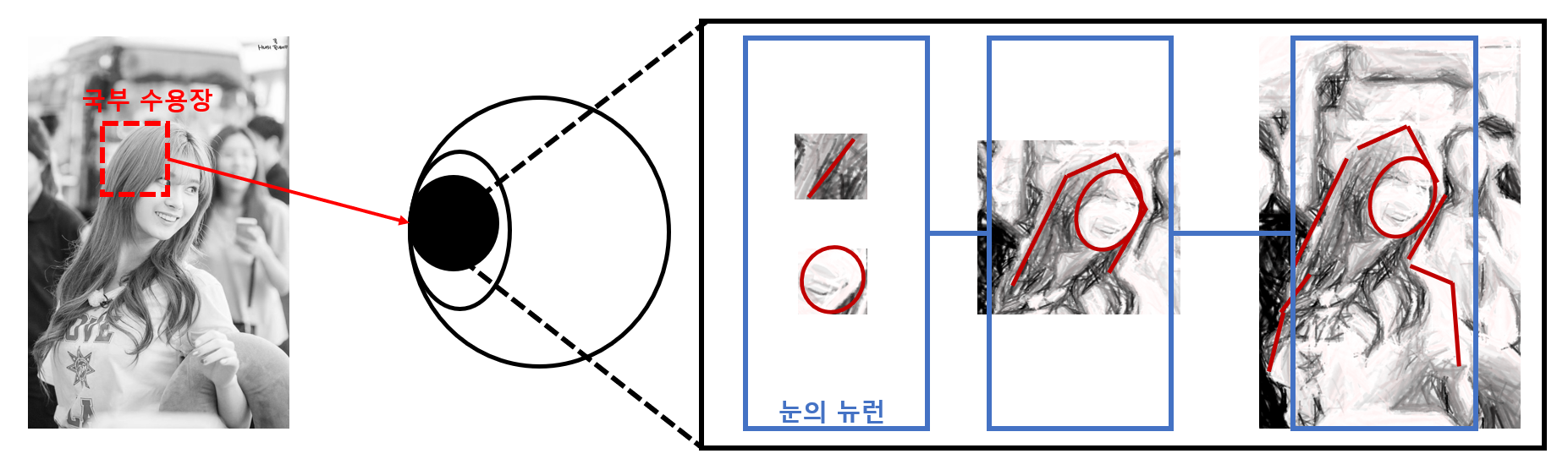
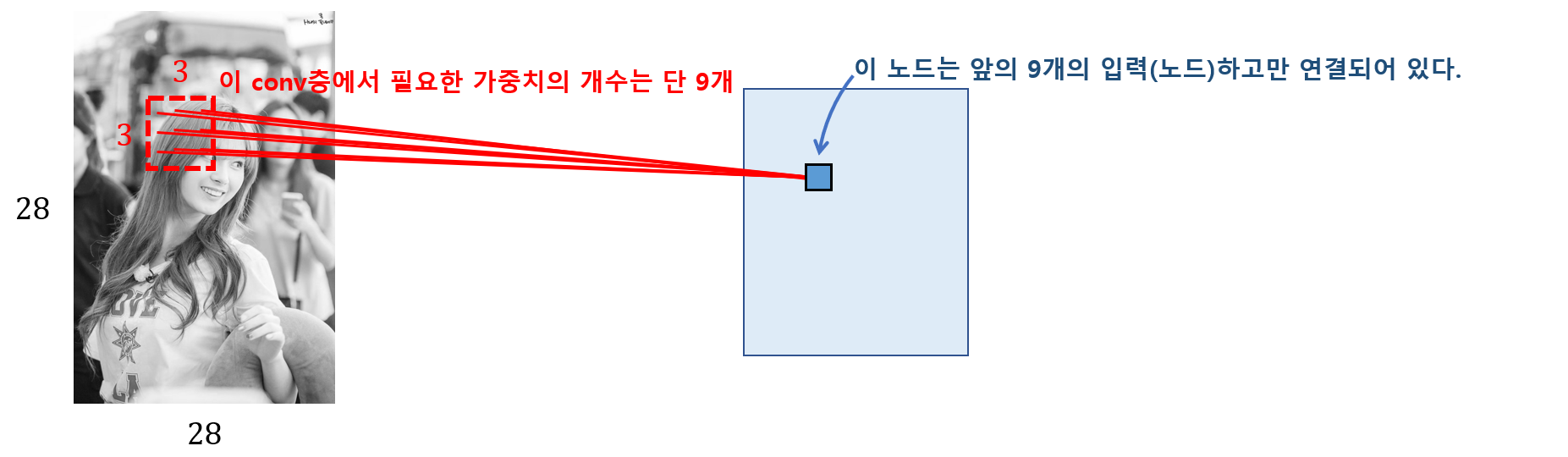
CNN은 눈의 원리와 비슷하다.
부분 연결 구조로 되어 있어 비교적 구해야 하는 가중치의 갯수가 적다.
학습 속도가 훨씬 빠르며, 과잉적합에 빠질 가능성 또한 낮아진다.
CNN 구조
보통 이미지 분류를 위한 CNN의 구조는 다음과 같습니다.
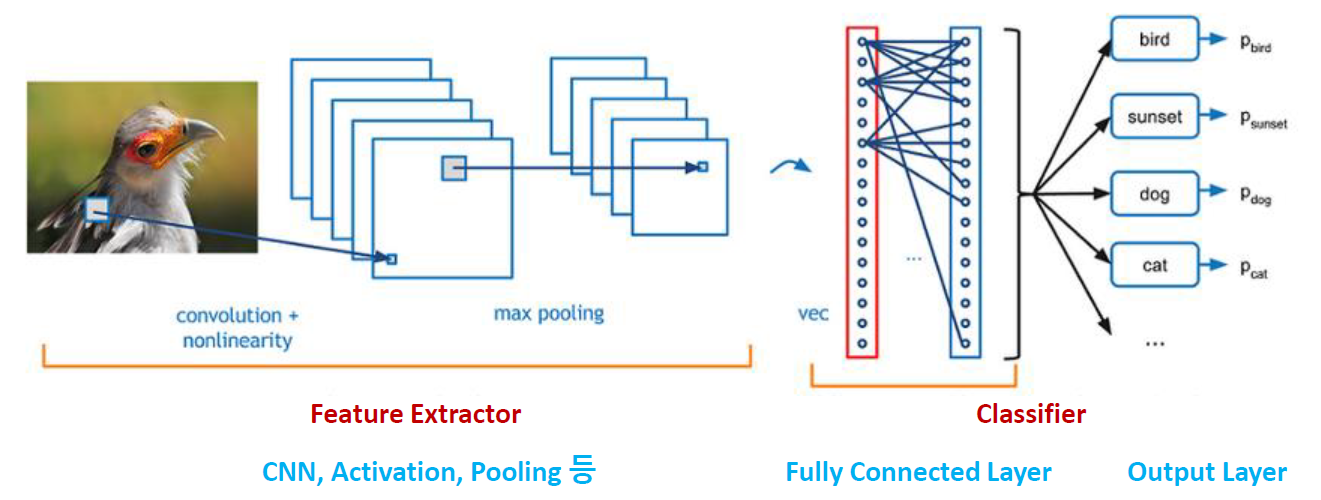
1. 컨볼루션 연산
사실 CNN에서의 합성곱은 실제의 합성곱과는 다릅니다. 실제의 합성곱은 필터를 뒤집어야 하지만 CNN에서는 필터를 뒤집지 않습니다. 그 이유는 어차피 필터의 가중치 값은 처음에 보통 랜덤으로 초기화하게 됩니다. 따라서 가중치를 굳이 뒤집지 않아도 상관이 없습니다. 어쨋든 CNN에서의 컨볼루션 연산은 필터가 옆으로 움직이면서 데이터와 각각 원소별 곱셈을 진행하고 그 곱셈의 결과들을 하나의 값으로 합하면 됩니다.
밑의 예시를 살펴보면 3×1 + 1×(-1) + 1×1 + 7×(-1) + 2×1 + 5×(-1) = -7 이 됩니다.
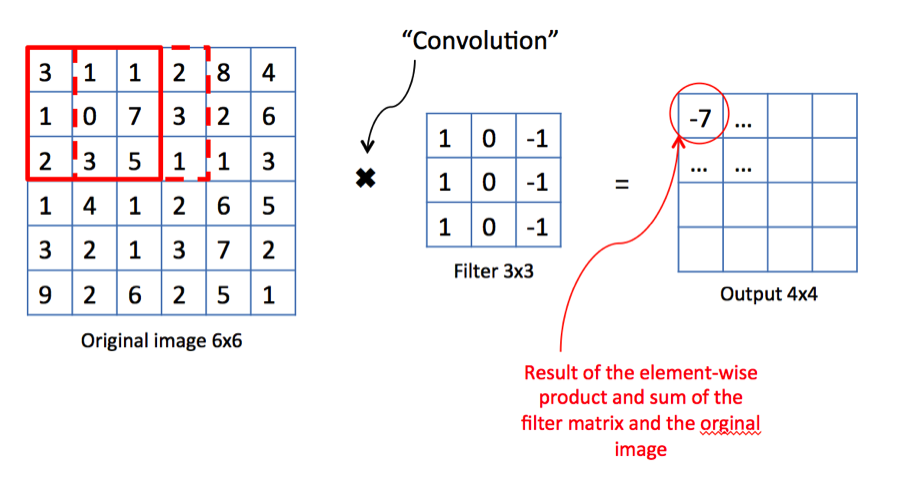
다음의 컨볼루션 연산은 필터의 사이즈, 스트라이드의 크기, 패딩 여부 등에 따라 결과(특성 맵)이 달라집니다.
2. 커널(채널), 필터
여기서 CNN에서 정말 헷갈리지만 또 중요한 개념이 등장합니다. 바로 커널(채널)과 필터입니다. 느낌이 비슷해서 헷갈릴 수 있지만 엄연히 구분되어 사용되어야 하기 때문에 여기서 한 번 짚고 넘어가도록 하겠습니다.
커널은 채널과 비슷한 의미로 데이터의 커널의 수(RGB채널의 경우 3)와 필터의 커널 수는 항상 같아야 합니다.
필터는 카메라 필터와 비슷하게 shape을 위한 필터, curve를 위한 필터와 같은 필터를 의미합니다.
예를 들어 채널이 1(Gray scale)이고 필터가 두 개인 경우 그림은 다음과 같습니다.
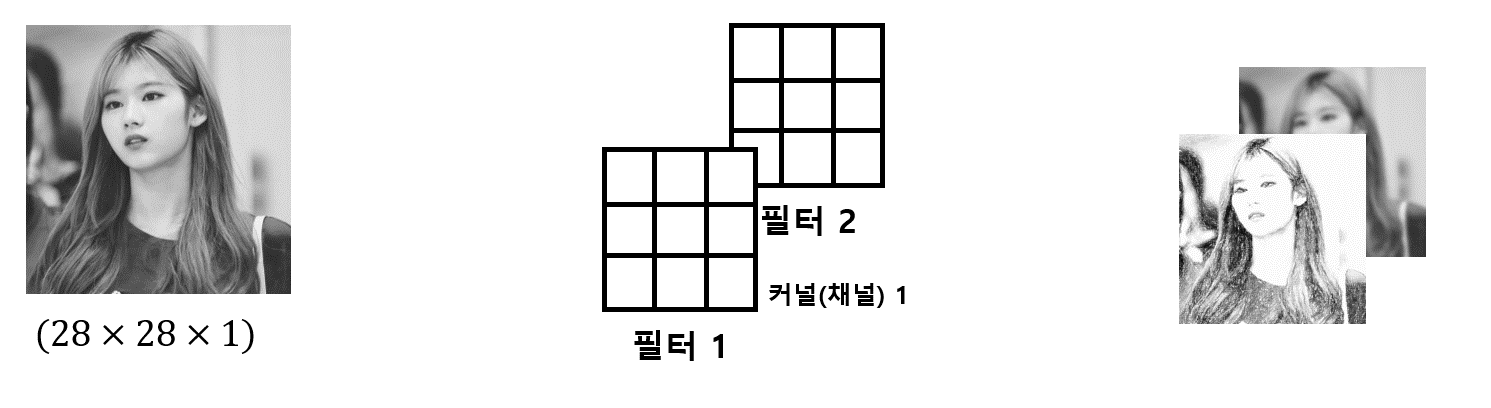
만약 채널이 3(RGB scale)이고 필터가 두 개인 경우 그림은 다음과 같습니다.
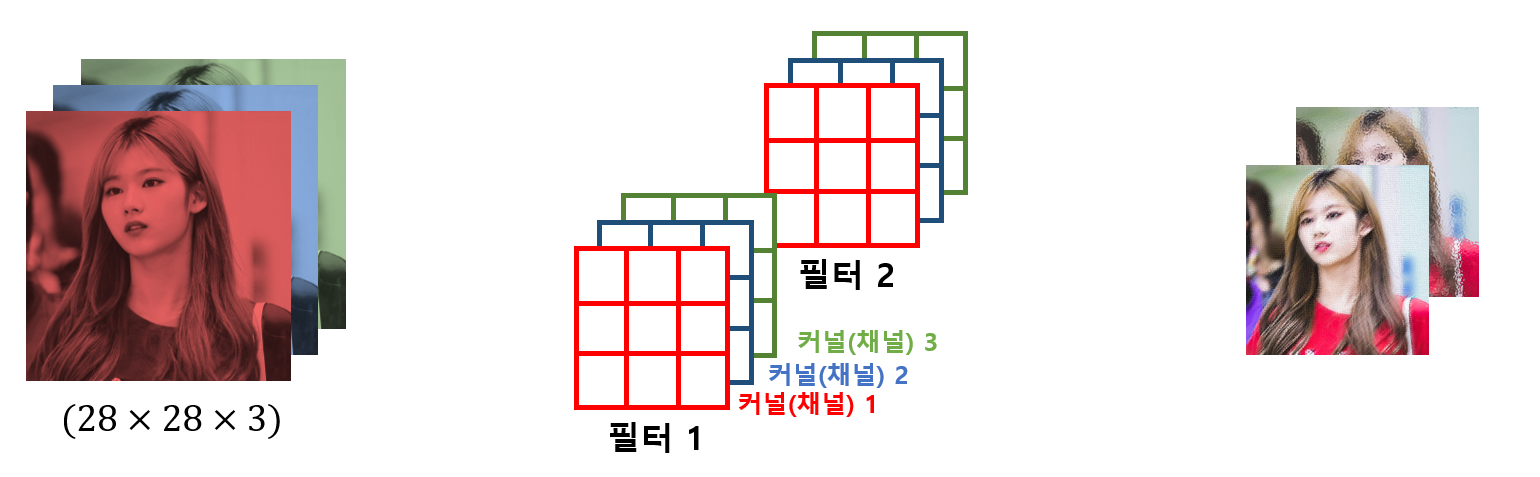
따라서 필터의 커널의 수는 항상 데이터의 커널의 수를 따르게 되고,
결과(특성 맵)의 커널 수는 항상 필터의 수를 따르게 됩니다.
CNN의 목표는 특징을 잘 추출해주는 필터의 가중치를 찾는 것입니다.
3. 스트라이드, 패딩
스트라이드(stride)
- 스트라이드는 필터의 미끄러지는 간격을 조절하는 것을 말합니다.
- 기본은 1이지만, 2를(2pixel 단위로 Sliding window 이동) 적용하면 입력 특성 맵 대비 출력 특성 맵의 크기를 대략 절반으로 줄여줍니다.
- stride 를 키우면 공간적인 feature 특성을 손실할 가능성이 높아지지만, 이것이 중요 feature 들의 손실을 반드시 의미하지는 않습니다.
- 오히려 불필요한 특성을 제거하는 효과를 가져 올 수 있습니다. 또한 Convolution 연산 속도를 향상 시킵니다.
패딩(padding)
- 패딩은 데이터 양 끝에 빈 원소를 추가하는 것을 말합니다.
-
패딩에는 밸리드(valid) 패딩, 풀(full) 패딩, 세임(same) 패딩이 있습니다. 패딩 각각의 역할은 다음과 같습니다.
패딩 역할 밸리드 평범한 패딩으로 원소별 연산 참여도가 다르다 풀 데이터 원소의 연산 참여도를 갖게 만든다 세임 특성 맵의 사이즈가 기존 데이터의 사이즈와 같도록 만든다 - 세임패딩을 적용하면 Conv 연산 수행 시 출력 특성 맵 이 입력 특성 맵 대비 계속적으로 작아지는 것을 막아줍니다.
4. 풀링 연산
- 풀링층은 특성 맵의 사이즈를 줄여주는 역할을 합니다.
- 보통 최대 풀링 또는 평균 풀링을 많이 사용합니다.
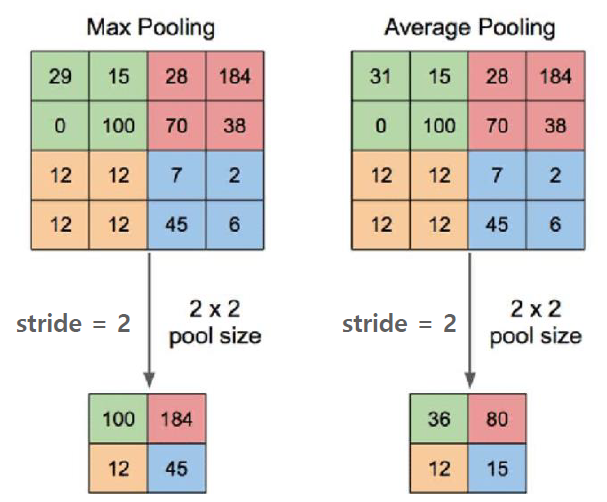
- 보통은 Conv연산, ReLU activation함수를 적용한 후에 풀링을 적용합니다.

- 풀링은 비슷한 feature 들이 서로 다른 이미지에서 위치가 달라지면서 다르게 해석되는 현상을 중화 시켜 줍니다.
- 일반적으로는 Sharp 한 feature 가 보다 Classification 에 유리하여 최대 풀링이 더 많이 사용됩니다.
- 풀링의 경우 특정 위치의 feature 값이 손실 되는 이슈로 인해 최근 Advanced CNN에서는 Stride만 이용하여 모델을 구성하는 경향입니다.
특성맵의 크기 구하기
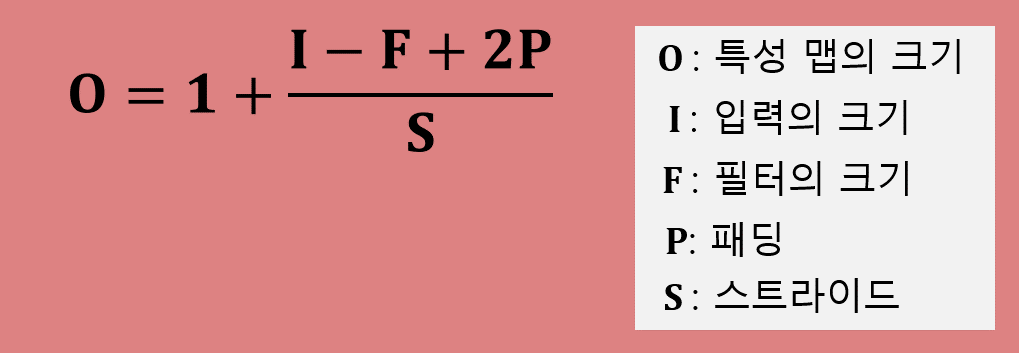
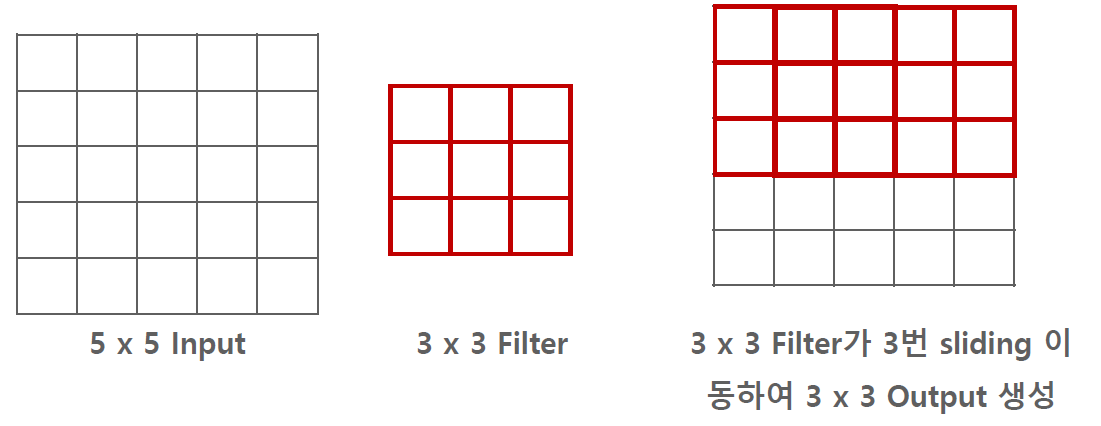
- 5×5 입력, 3×3 필터가 스트라이드가 1이고 패딩이 없는 경우, 특성 맵의 크기는 3×3이 됩니다.
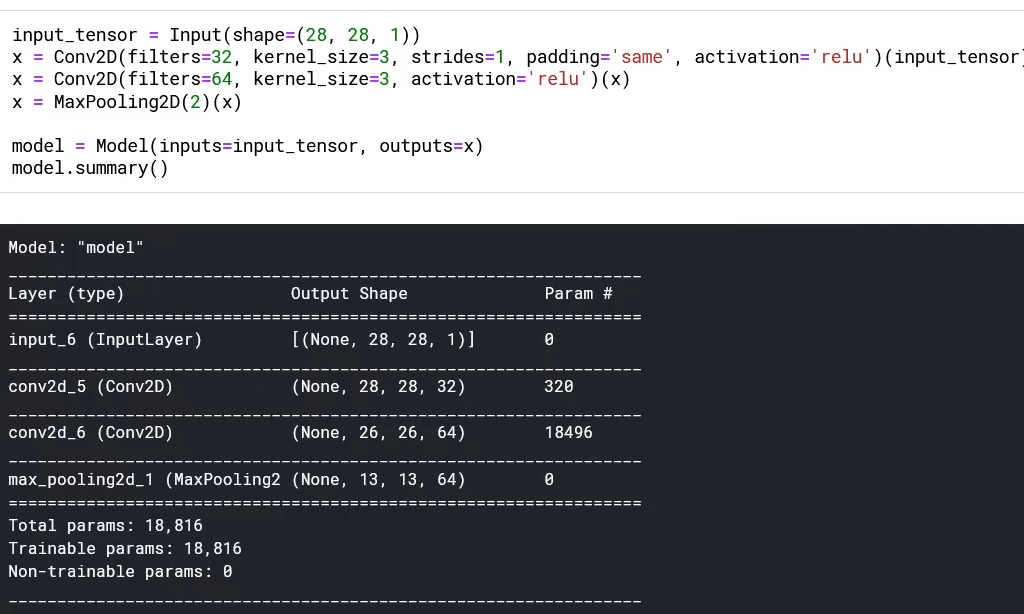
CNN 모델의 구조에 따른 파라미터 수와 특성 맵 차원 생각해보기