분류(Logistic regression)

1. 로지스틱 회귀(Logistic regression)

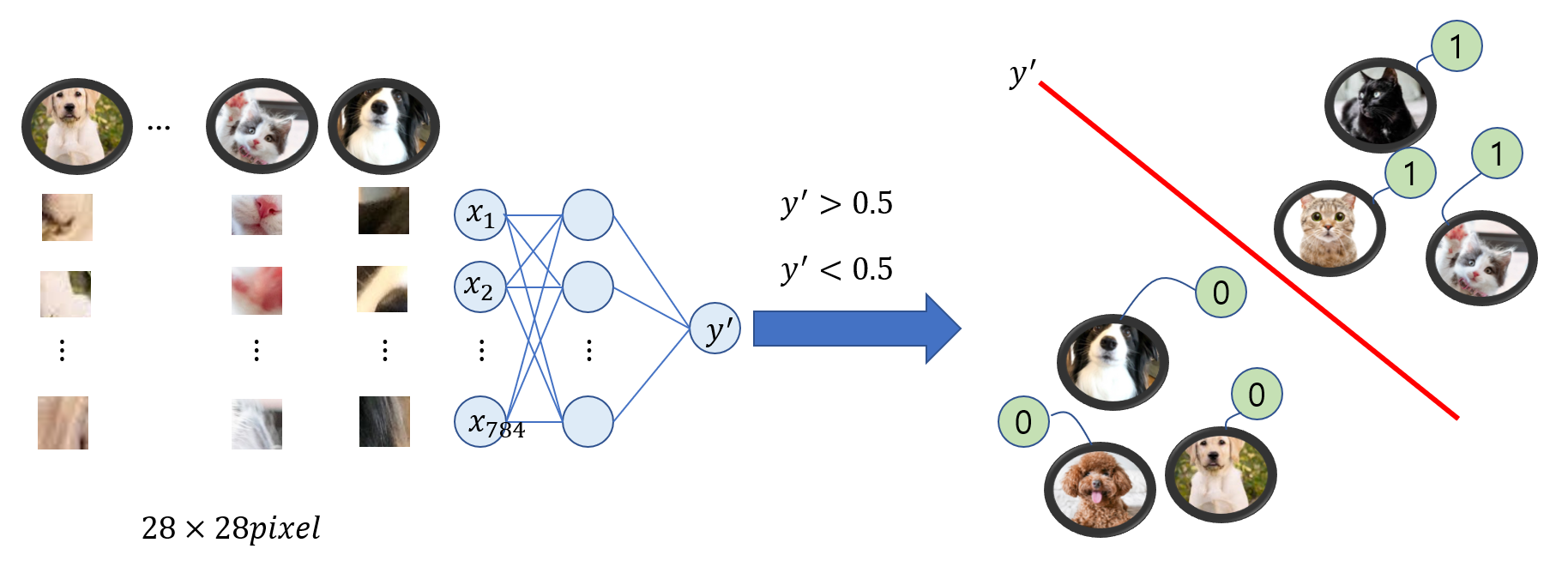
앞에서 연속적인 값을 예측하는 모델에 대해 공부했습니다. 이번 포스트에서는 고양이, 개를 분류하는 이진 분류, 2가지 이상을 분류하는 다중 분류에 대해 공부해 보겠습니다. 그럼 회귀가 아니라 분류라고 해야 하지 않는가? 왜 로지스틱 회귀라고 할까? 여기서부터는 저의 생각이니 편하게 보고 그냥 넘기셔도 됩니다. 우선 로지스틱 회귀는 앞에서 봤던 회귀 모델과 같이 연속적인 값을 예측합니다. 다만 뒤에 시그모이드 함수와 합성함수를 취해주게 됩니다. 그럼 결과는 어떨까요? 시그모이드 함수의 결과는 0과 1사이의 실수값입니다. 그렇기 때문에 여전히 연속적인 값을 예측하는 것이라는 점에서 회귀라고 할 수 있는 것이지요. 다만 0과 1 사이의 값을 리턴하니까 예를 들면, 다음 사진이 고양이인지 아닌지에 대한 확률로 이용할 수 있을 것 같다는 생각이 듭니다. 그렇기 때문에 로지스틱 회귀라는 회귀 모델이지만 분류에 사용되는 것 같습니다.

로지스틱 회귀는 0과 1사이의 실수값을 리턴해주므로 회귀다
0과 1사이의 값을 분류를 위한 확률로 사용될 수 있기에 분류 모델에 사용된다.

고양이, 개 사진 분류하기

2. 활성화 함수: 시그모이드(Sigmoid)

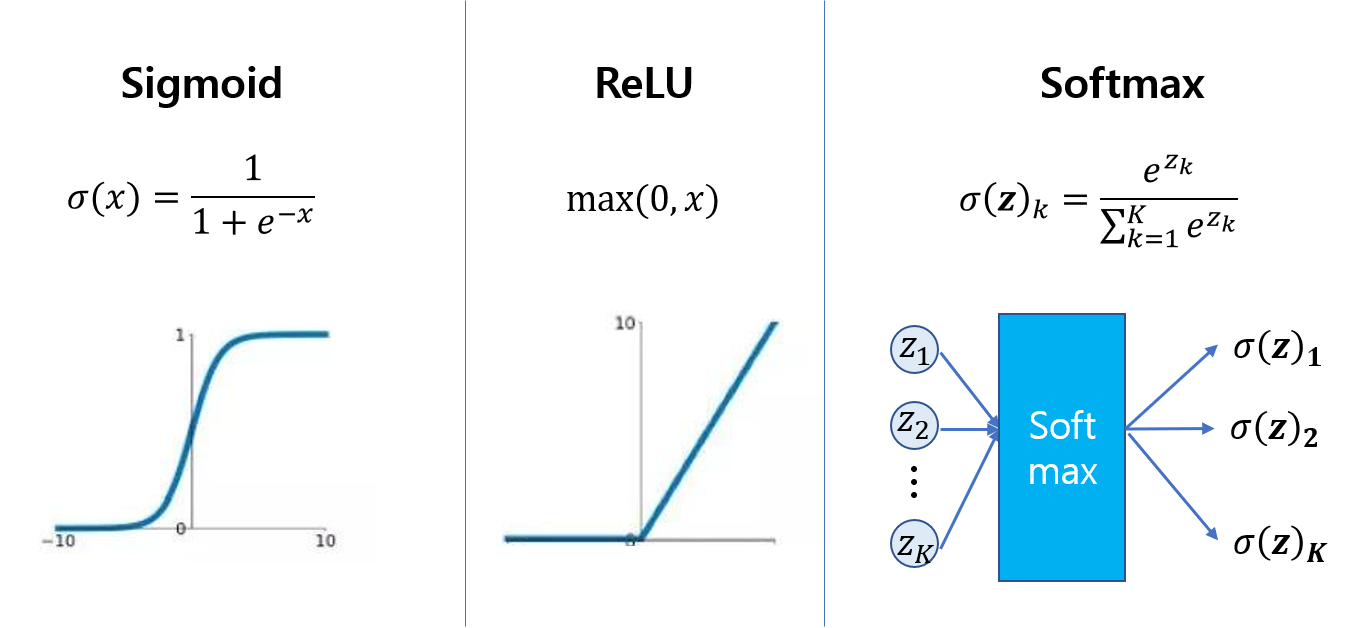
여기서부터 인공지능에서 중요한 개념 중 하나인 활성화 함수에 대해 알아보겠습니다. 활성화 함수의 종류는 다양합니다. 그 중 여기서는 Sigmoid 함수에 대해 알아보겠습니다. 그 밖에도 대표적으로 ReLU(Rectified Linear Unit) 함수가 있으면 ReLU는 최근 딥러닝에 많이 사용되는 대표적인 활성화 함수입니다.
Sigmoid 함수는 0과 1사이의 연속적인 값을 리턴하기 때문에 확률로 사용하기 적합합니다. 그래서 이진 분류의 출력층에 활성화 함수로 많이 사용됩니다. ReLU 함수는 값이 0또는 입력값(x)이기 때문에 미분 계산 다른 활성화 함수보다 훨씬 간단합니다. 그러한 이유로 은닉층에 많이 이용되고 있습니다.

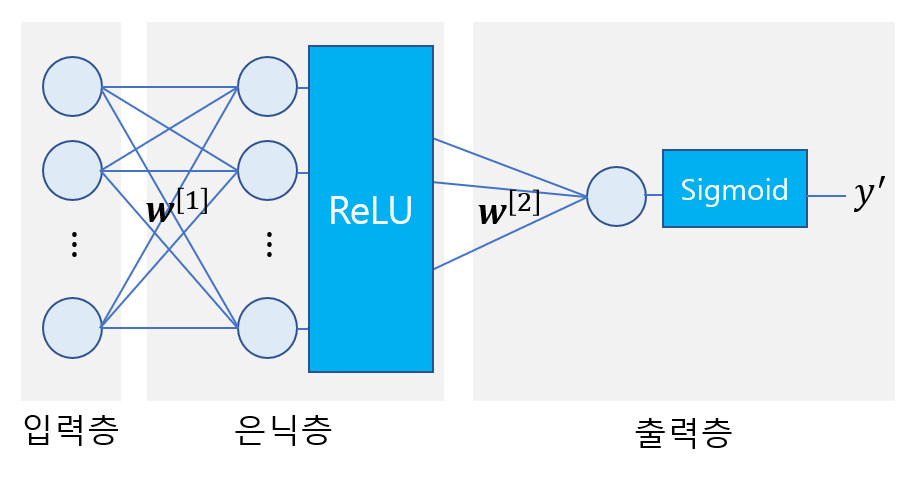
보통 각 층에 있는 노드는 서로 같은 활성화 함수를 사용합니다. 밑에 그림은 입력층과 은닉층에는 ReLU함수를 사용했고, 출력층에는 이진 분류를 위해 Sigmoid함수를 사용하였습니다.

은닉층에 활성화 함수가 없다면 층을 깊게 쌓아도 결국 가중치와 데이터의 곱과 합의 형태를 갖는 하나의 층에 불과하기 때문에 각 은닉층에는 ReLU와 같은 활성화 함수를 사용해야 층을 깊게 쌓는 의미가 있게 됩니다.

활성화 함수는 각 층마다 활성화 함수를 가지고 있다.

만약 각 층 간에 활성화 함수가 없다면 층이 깊어져도 선형 함수이기 때문에 층이 깊어져도 의미가 없다.

보통 각 은닉층에는 ReLU함수가 사용되고, 이진 분류를 위해 출력층에는 Sigmoid 함수가 사용된다.

다중 분류에는 출력층으로 Softmax 함수가 사용된다.

3. 손실 함수: 크로스 엔트로피(Cross entropy)

앞에서 최종적으로 모델의 예측 값을 얻었습니다. 이제 우리가 얻은 값과 실제 값 사이를 비교해 최적화를 하기 위해 손실 함수를 정의 해야 합니다.
이 전 회귀 모델에서는 MSE를 사용했습니다. 분류를 위한 손실 함수로는 어떤 것을 선택하는 것이 좋을까요? 그대로 MSE를 쓴다면 어떨지 먼저 생각해봅시다.

선형 회귀는 정답과 예상값의 오차 제곱이 최소가 되는 가중치를 찾는 것이 목표였습니다. 그렇다면 분류의 목표는 무엇일까요? 올바르게 분류된 데이터의 비율을 높이는 것이 분류의 목표입니다. 하지만 올바르게 분류된 샘플의 비율은 미분 가능한 함수가 아니기 때문에 경사 하강법의 손실 함수로 사용할 수가 없습니다. 대신 비슷한 역할을 하는 함수가 있습니다. 바로 그 함수가 로지스틱 손실 함수입니다.

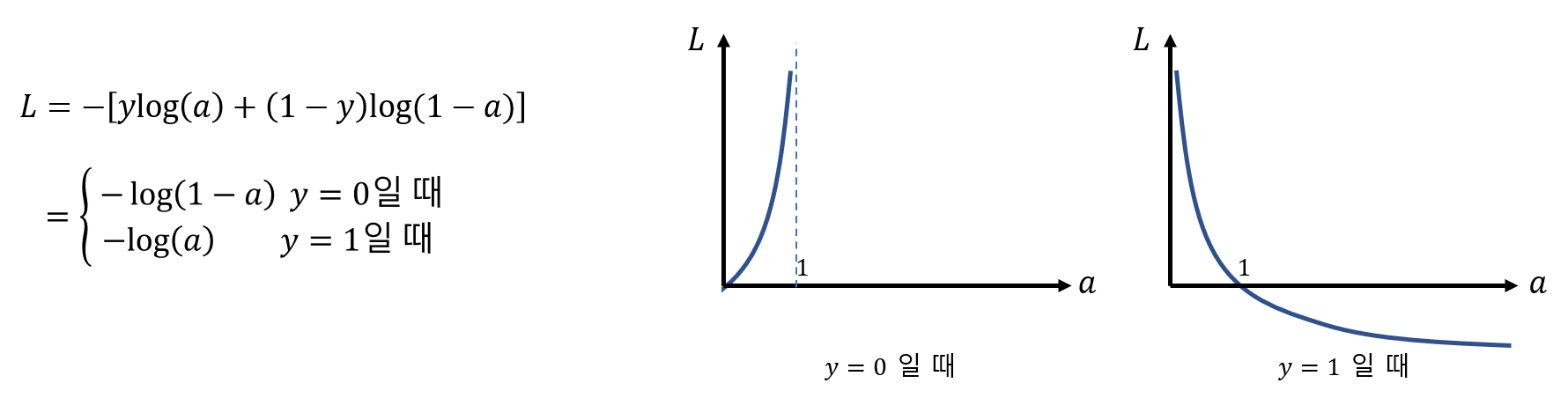
이진 분류를 위한 크로스 엔트로피 함수

다중 분류를 위한 크로스 엔트로피 함수

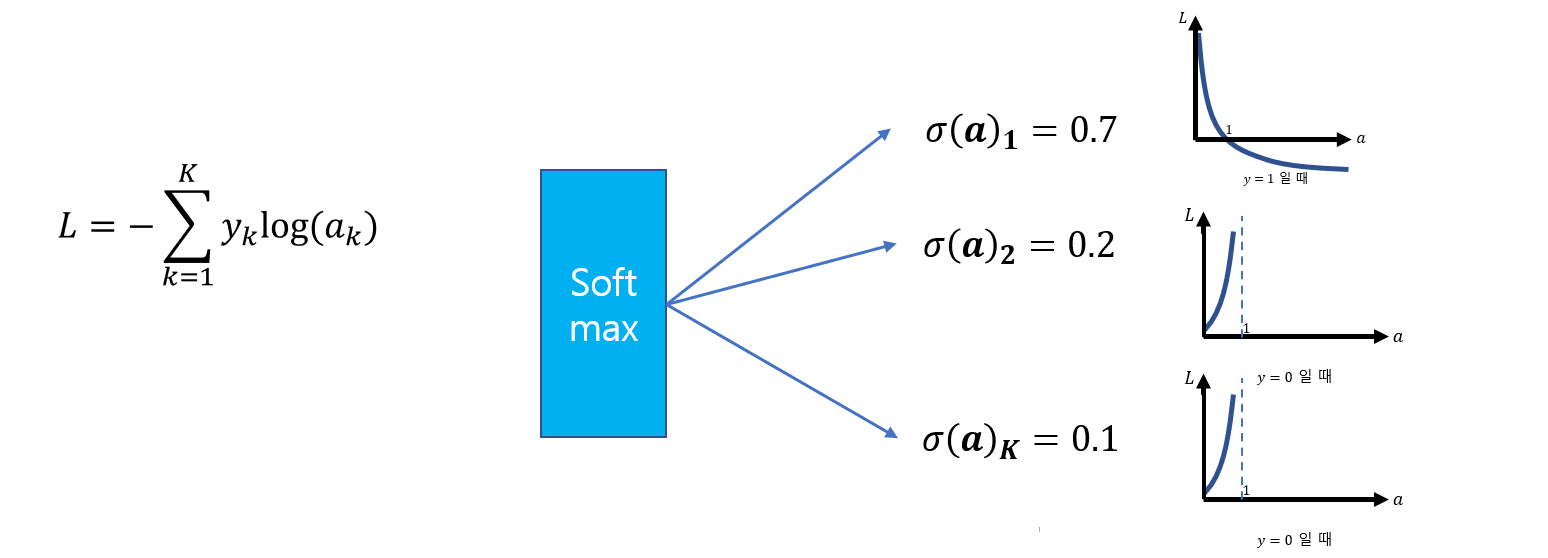
정답이 0인 경우 우리의 출력값이 1에 가까워지면 손실함수가 증가하게 됩니다. 반면에 정답이 1인 경우에는 출력값이 0에 가까워 질수록 손실함수가 증가합니다.

4. 가중치 업데이트

선형 회귀 모델에서는 가중치를 업데이트 할 때 손실함수를 바로 가중치에 대해 미분할 수 있었다. 하지만 실제로 은닉층이 생기고 활성화 함수가 추가되면 더 이상 바로 미분할 수가 없다. 그래디언트를 구하기 위해서는 우선 활성화 함수에 대해 편미분을 해야한다. 이렇게 합성함수를 순서대로 편미분해 곱한 것을 Chain rule이라고 한다.

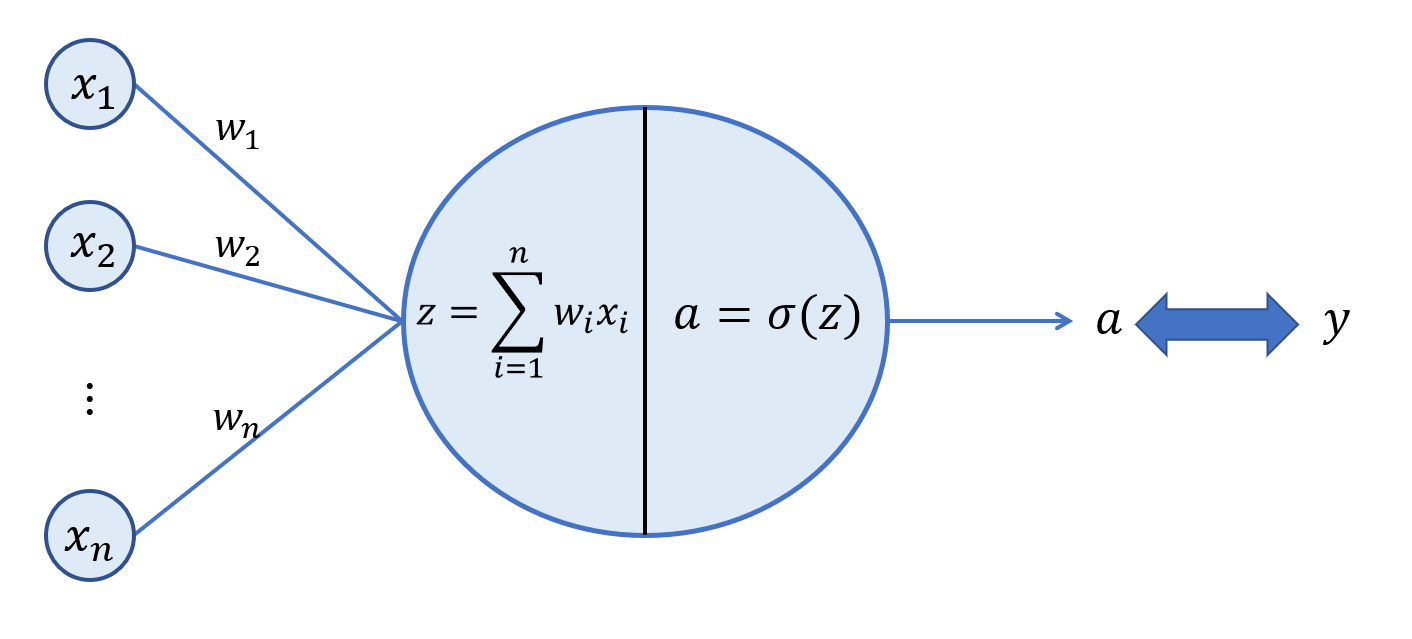
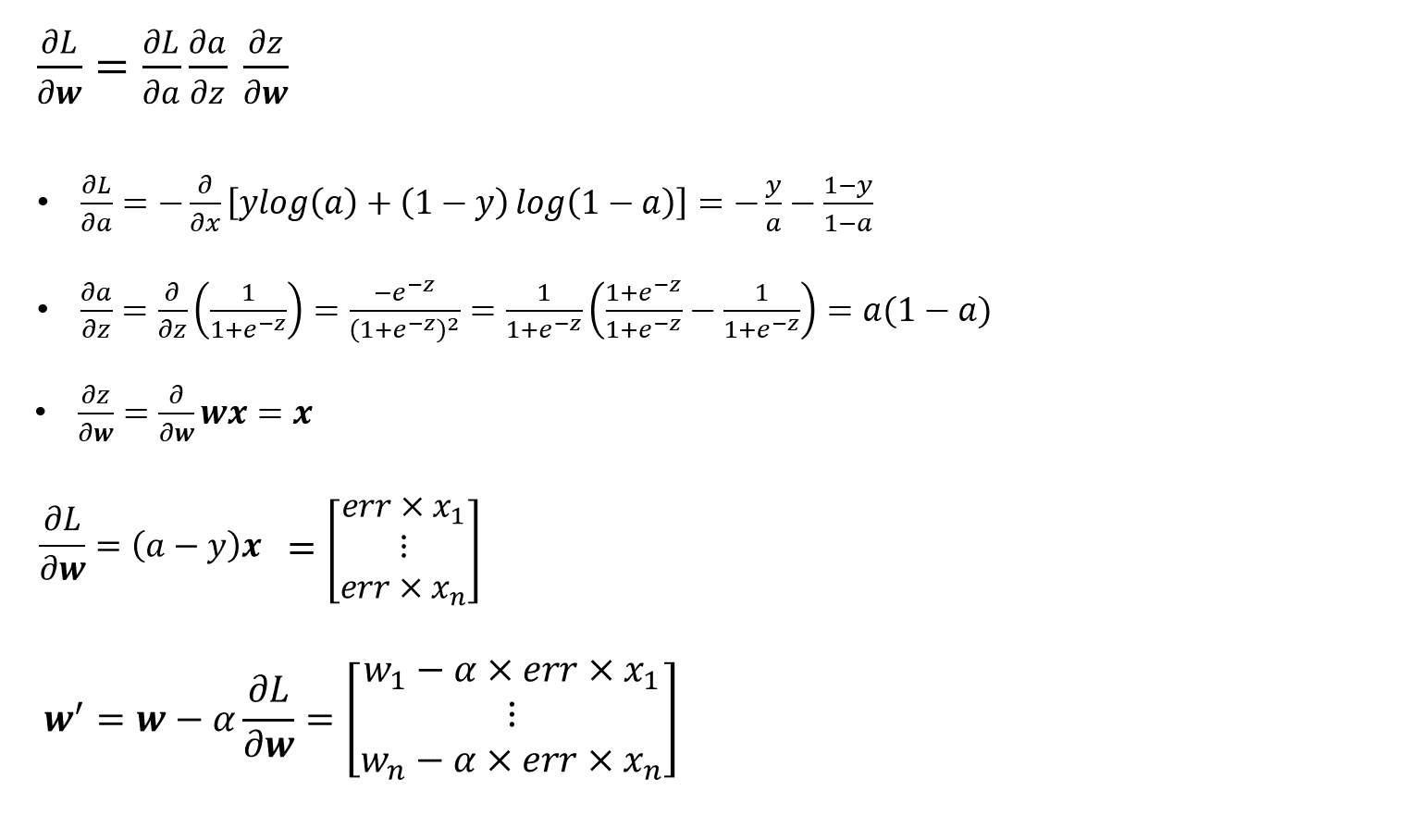
과정은 선형회귀보다 조금 복잡하지만 결과는 같게 나왔다.

크로스 엔트로피 손실함수를 활성화 함수를 고려해 그래디언트를 구한 결과 여전히 err*x 이다.