선형 회귀
1. 선형 회귀(Linear regression)
딥러닝을 배울 때 출발점으로 좋은 모델이 바로 선형 회귀입니다. 왜냐하면 뒤에서 배우게 될 모델들은 보통 이러한 선형 회귀에서 약간 변형하고, 추가하는 방법을 통해 만들어 지기 때문입니다.
선형 회귀에서
선형: 모델이 가중치와 데이터의 곱과 합으로 구성되어 있다. 이러한 경우를 데이터의 선형 조합(linear combination)이라고 한다.
회귀: 어떤 연속적인 값을 예측하는 것을 회귀 라고 한다.
선형 회귀 모델
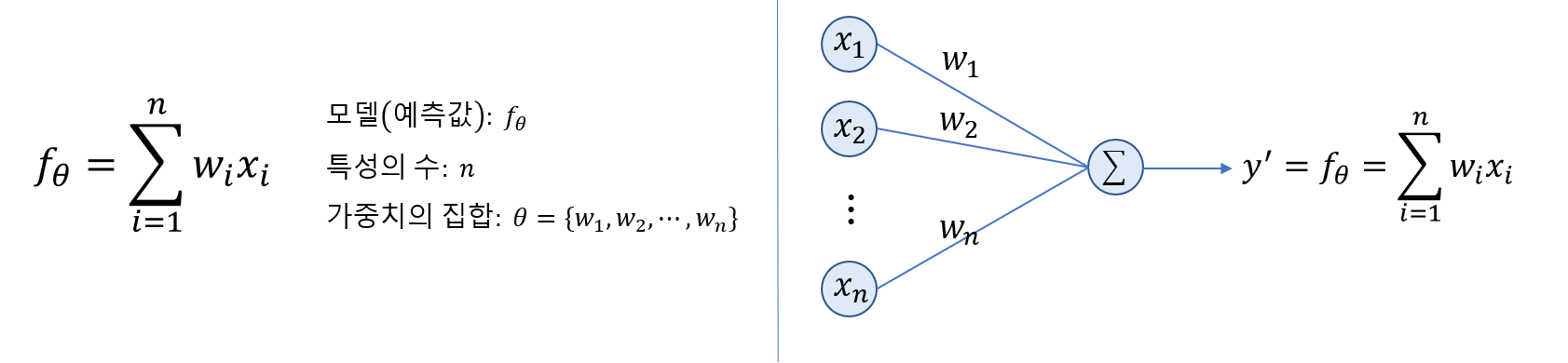
2. 손실함수: MSE(Mean Squared Error)
우리의 모델의 예측 값(y’)이 정답(y)에 가깝도록 하는 것이 목표일 때 손실함수를 어떻게 정의하면 좋을까? 바로 머릿 속에 떠오르는 방법은 둘 간의 오차로 정의하는 것입니다. 이것을 우리는 Error라고 한다. 근데 Error 값은 양수일 수도 있고, 음수일 수도 있습니다. 그 상태에서 Error들을 합하면 실제 우리가 생각하는 것보다 작을 것입니다.
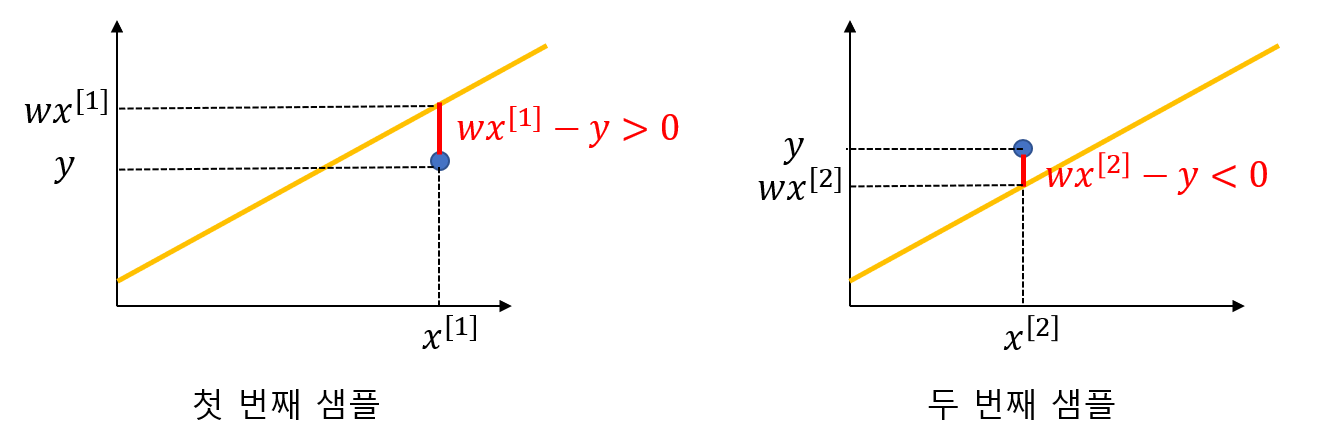
그렇기 때문에 항상 각각의 Error가 양수가 되도록 제곱을 취하도록 하겠습니다. 이것을 우리는 MSE라고 합니다. 아마 더 깊이 공부하다 보면 이런 MSE 손실함수로는 부족할 수 도 있다고 생각이 듭니다. 하지만 MSE는 처음에 인공지능을 시작할 때 사용하기 좋은 손실함수이기 때문에 여기서는 회귀 모델에서는 MSE를 손실함수로 사용한다 라고 까지만 하고 마치도록 하겠습니다.
MSE를 통해 정의한 손실함수 L
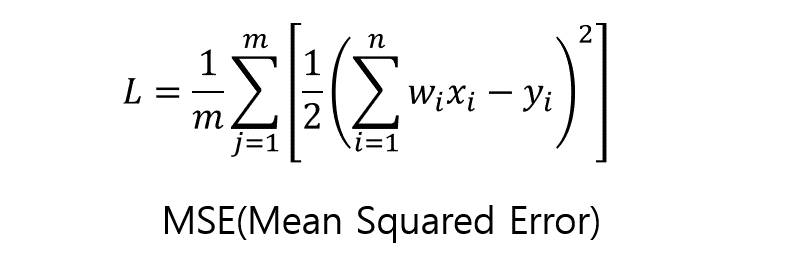
3. 가중치 업데이트
가중치(w)를 업데이트해 우리의 모델을 최적화시켜보도록 하겠습니다. 앞에서 우리는 가중치를 업데이트 하는 방법으로 경사하강법(Gradient descent)를 사용한다고 했습니다. 그렇기 때문에 우선 각 가중치의 Gradient를 구해야합니다. 그리고 Gradient는 함수값을 가장 가파르게 증가하는 방향이므로 (-)를 취해 손실함수 값을 가장 빠르게 감소시키는 방향으로 가중치를 업데이트 하겠습니다.
손실함수를 각각의 가중치에 대해 편미분한다.
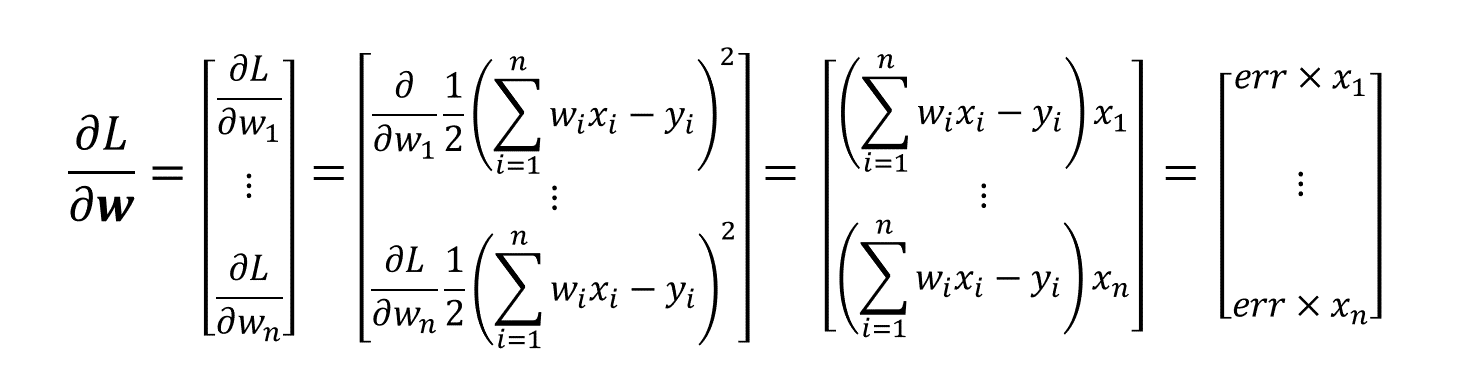
각각의 편미분에 (-)를 취해 해당 가중치 지점에서 가장 빨리 손실함수를 감소시키는 방향으로 가중치를 업데이트한다.
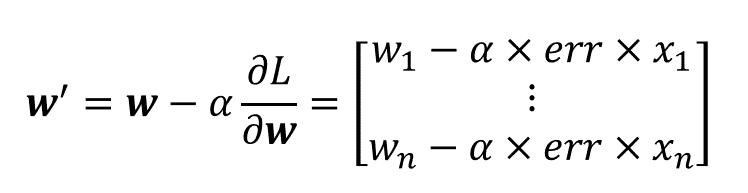
(알파는 학습률이라는 파라미터인데 얼마나 크게/작게 가중치를 업데이트할 것인지 정하는 값이다.)
