수학, 축 방향

1. 넘파이 연산

넘파이는 element-wise연산하는 vectorization을 지원하기 때문에 루프 없이 계산할 수 있어 리스트보다 코드도 간결하고 실행 속도 또한 빠릅니다.

>>> A = np.array([1, 2, 3])
>>> B = np.array([3, 3, 3])

>>> C = A+B  
>>> C
array([0, 0, 0])  

>>> C = A*3
>>> C
array([3, 6, 9])

#행렬 곱
np.matmul()	

# 점 곱
np.dot()

# 텐서 곱
np.cross()

# 내적
np.inner()

# 외적
np.outer()

# 전치
np.transpose()

np.sum()

np.cumsum()

np.prod()

np.cumprod()

np.abs( array )	요소별 절댓값
np.round( array )	요소별 반올림
np.ceil( array )	요소별 올림
np.floor( array )	요소별 내림
np.trunc( array )	요소별 절사
np.maximum( array1, array2 )	요소별 최댓값
np.minimum( array1, array2 )	요소별 최솟값
np.max( array )	배열의 최댓값
np.min( array )	배열의 최솟값
np.argmax( array )	배열의 최댓값의 색인
np.argmin( array )	배열의 최솟값의 색안

np.add( array1, array2 )	요소별 덧셈
np.subtract( array1, array2 )	요소별 뺄셈
np.multiply( array1, array2 )	요소별 곱셈
np.divide( array1, array2 )	요소별 나눗셈
np.power( array1, array2 )	요소별 제곱
np.sqrt( array )	요소별 제곱근
np.mod( array1, array2 )	요소별 나눗셈의 나머지

np.sin( array )	요소별 사인
np.cos( array )	요소별 코사인
np.tan( array )	요소별 탄젠트
np.arcsin( array )	요소별 아크 사인
np.arccos( array )	요소별 아크 코사인
np.arctan( array )	요소별 아크 탄젠트
np.sinh( array )	요소별 하이퍼볼릭 사인
np.cosh( array )	요소별 하이퍼볼릭 코사인
np.tanh( array )	요소별 하이퍼볼릭 탄젠트

np.greater( array1, array2 )	요소별 array1 > array2 연산
np.greater_equal( array1, array2 )	요소별 array1 >= array2 연산
np.less( array1, array2 )	요소별 array1 < array2 연산
np.less_equal( array1, array2 )	요소별 array1 <= array2 연산
np.equal( array1, array2 )	요소별 array1 == array2 연산
np.not_equal( array1, array2 )	요소별 array1 != array2 연산

np.logical_and( array1, array2 )	요소별 Boolean 자료형 논리 AND 연산
np.logical_or( array1, array2 )	요소별 Boolean 자료형 논리 OR 연산
np.logical_xor( array1, array2 )	요소별 Boolean 자료형 논리 XOR 연산
np.logical_not( array )	요소별 Boolean 자료형 논리 NOT 연산

2. 배열의 통계적 특성

>>> arr = np.array([1, 2, 3, 4, 5, 6]) 

>>> arr.min()
1

>>> arr.max()
6

>>> arr.mean()
3.5

>>> arr.sum()
21

3. 계산할 차원 방향 지정하기

>>> arr = np.array([[1, 2], [3, 4]])
>>> arr
array([[1, 2],
        3, 4])

>>> arr.sum(axis=0)
array([4, 6])

>>> arr.sum(axis=0).shape
(2, )

>>> arr.sum(axis=1)
array([3, 7])

>>> arr.sum(axis=1).shape
(2, )

4. 배열의 축

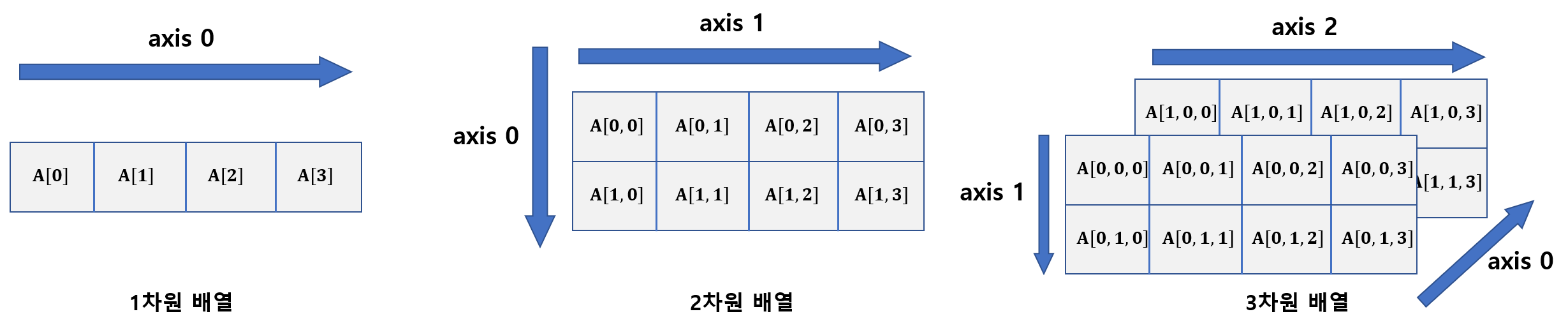
1) 축을 기준으로 연산한 배열의 shape

축(axis)	shape
기존	(2,2,4)
axis 0	(2, 4)
axis 1	(2,4)
axis 2	(2,2)

>>> arr = np.array([[[1, 2, 3, 4],[5, 6, 7, 8]],[[1, 2, 3, 4],[5, 6, 7, 8]]])

>>> arr.sum(axis=0)
array([[ 2,  4,  6,  8],
       [10, 12, 14, 16]])

>>> arr.sum(axis=1)
array([[ 6,  8, 10, 12],
       [ 6,  8, 10, 12]])
>>> arr.sum(axis=2)
array([[10, 26],
       [10, 26]])

2) 축 추가

>>> arr = np.array([1, 2, 3, 4])
>>>arr.shape
(4, )

>>> arr_2 = arr[np.newaxis]
>>> arr_2.shape
(1, 4)

>>> arr_3 = arr[:, np.newaxis]
>>> arr_3
(4, 1)

3) 차원 확장 및 축소

>>> a = np.array([1, 2, 3])
>>> a
array([1, 2, 3])

>>> a.shape
(3, )

>>> b = np.expand_dims(a, axis=0)
>>> b
array([[1, 2, 3]])

>>> b.shape
(1, 3)

>>> c= np.expand_dims(a, axis=1)
>>> c
array([[1], [2], [3]])

>>> c.shape
(3, 1)

>>> b_prime = np.squeeze(b)
>>> b_prime
array([1, 2, 3])

>>> b_prime.shape
(3, )

4) 1차원 배열 사용시 주의점

1차원 배열의 shape속성을 출력해보면, 튜플의 두 번째 원소 자리가 공백으로 남겨진 채 출력됩니다. 행벡터라면(1,x), 열벡터라면(x,1)의 shape을 가져야 할 것 같지만, 넘파이에서는 1차원 배열의 경우 행벡터와 열벡터 구분 없이 사용됩니다.

shape을 (1,4) 또는 (4,1)로 하고 싶다면,

>>> arr = np.array([1, 2, 3, 4])

>>> a.shape = 1,4
>>> a
array([[1, 2, 3, 4]])

>>> a.shape = 4,1
>>> a
array([[1],
       [2],
       [3],
       [4]])

5. 정렬

# 원래 행렬은 그대로 두고, 정렬된 행렬 리턴 
np.sort() 

# 내림차순 정렬
np.sort()[::-1]

# 원래 행렬을 정렬 
ndarray.sort()

# 2차원 배열의 axis를 이용한 sort()

A = np.array([[8, 12], [7, 1]])

np.sort(A, axis = 0)
-----------------------------
array([[7, 1], [8, 12]])

# 정렬된 행렬의 바뀐 인덱스를 리턴
np.argsort()

A = np.array([3, 1, 9, 5])

np.argsort(A)
----------------------------
array([1, 0, 3, 2])